Question

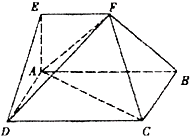如图，在多面体ABCDEF中，四边形ABCD是矩形，AB∥EF，∠EAB=90°，AB=2，AD=AE=EF=1，平面ABFE⊥平面ABCD．
（1）求证：面DAF⊥面BAF．
（2）求钝二面角B-FC-D的大小．

Answer 1

分析：（1）要证两个平面互相垂直，只要证明其中一个平面经过另一个平面的一条垂线即可，由四边形ABCD是矩形可知AD⊥AB，再由平面ABFE⊥平面ABCD可得AD⊥平面BAF，则结论得证；
（2）分别以AD，AB，AE所在直线为x轴，y轴，z轴，建立的空间直角坐标系，标出用到的点的坐标，求出两个平面BFC与CFD的一个法向量，利用平面法向量所成的角求二面角的大小．

解答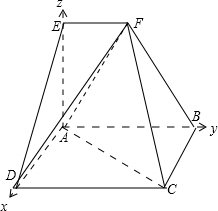：（1）证明：如图，
∵平面ABFE⊥平面ABCD，AD⊥AB，
∴AD⊥平面BAF．
又∵AD?面DAF，
∴面DAF⊥面BAF；
（2）解：分别以AD，AB，AE所在直线为x轴，y轴，z轴，建立的空间直角坐标系，
则A（0，0，0）、D（1，0，0）、C（1，2，0）、E（0，0，1）、B（0，2，0）、F（0，1，1）
∵

DC

=(0，2，0)，

DE

=(-1，0，1)，
设

n

=(x，y，z)为平面CDFE的一个法向量，则

n • DC =0 n • DE =0

，

2y=0 -x+z=0

，令x=1，得z=1，
所以

n

=(1，0，1)．
由平面ABEF⊥平面ABCD知，AF⊥BC，在△AFB中，AF=

2

，AB=2，BF=

2

，∴AF⊥面FBC．
∴

m

=

AF

=(0，1，1)为平面BCF的一个法向量，
∴cos＜

m

，

n

＞=

m • n

| m |•| n |

=

1

2

，
∵二面角B-FC-D的平面角为钝角，
∴钝二面角B-FC-D的大小120°．

点评：本题考查了平面与平面垂直的判定，考查了利用空间向量求二面角的大小，解答的关键在于建立正确的空间右手直角坐标系，是中档题．