题目内容
某汽车生产企业上年度生产一品牌汽车的投入成本为10万元/辆,出厂价为13万元/辆,年销售量为5000辆.本年度为适应市场需求,计划提高产品档次,适当增加投入成本,若每辆车投入成本增加的比例为x(0<x<1),则出厂价相应提高的比例为0.7x,年销售量也相应增加.已知年利润=(每辆车的出厂价-每辆车的投入成本)×年销售量.(Ⅰ)若年销售量增加的比例为0.4x,为使本年度的年利润比上年度有所增加,则投入成本增加
的比例x应在什么范围内?
(Ⅱ)年销售量关于x的函数为y=3240(-x2+2x+
| 5 | 3 |
分析:(Ⅰ)根据题意,要使本年度的年利润比上年度有所增加,则投入成本增加的比例x应在什么范围内?首先表示出本年度的年利润,根据原题中已知的年利润=(每辆车的出厂价-每辆车的投入成本)×年销售量可表示出来.然后列出不等式得到x的取值范围.
(Ⅱ)根据题意,要使本年度的年利润最大,首先表示出本年度年利润的函数表达式,然后求出此函数的导数为零时x的值,并且考虑导数大于零和小于零时函数的增减性可知此时的x值对应的函数值是函数的最值.
(Ⅱ)根据题意,要使本年度的年利润最大,首先表示出本年度年利润的函数表达式,然后求出此函数的导数为零时x的值,并且考虑导数大于零和小于零时函数的增减性可知此时的x值对应的函数值是函数的最值.
解答:解:(Ⅰ)由题意得:本年度每辆车的投入成本为10×(1+x);
出厂价为13×(1+0.7x);年销售量为5000×(1+0.4x),
因此本年度的利润为
y=[13×(1+0.7x)-10×(1+x)]×5000×(1+0.4x)
=(3-0.9x)×5000×(1+0.4x)
=-1800x2+1500x+15000(0<x<1),
由-1800x2+1500x+15000>15000得0<x<
(Ⅱ)本年度的利润为f(x)=(3-0.9x)×3240×(-x2+2x+
)=3240×(0.9x3-4.8x2+4.5x+5)
则f′(x)=3240×(2.7x2-9.6x+4.5)=972(9x-5)(x-3),
由f′(x)=0,解得x=
或x=3,
当x∈(0,
)时,f′(x)>0,f(x)是增函数;当x∈(
,1)时,f′(x)<0,f(x)是减函数.
∴当x=
时,f(x)取极大值f(
)=20000万元,
因为f(x)在(0,1)上只有一个极大值,所以它是最大值,
所以当x=
时,本年度的年利润最大,最大利润为20000万元.
出厂价为13×(1+0.7x);年销售量为5000×(1+0.4x),
因此本年度的利润为
y=[13×(1+0.7x)-10×(1+x)]×5000×(1+0.4x)
=(3-0.9x)×5000×(1+0.4x)
=-1800x2+1500x+15000(0<x<1),
由-1800x2+1500x+15000>15000得0<x<
| 5 |
| 6 |
(Ⅱ)本年度的利润为f(x)=(3-0.9x)×3240×(-x2+2x+
| 5 |
| 3 |
则f′(x)=3240×(2.7x2-9.6x+4.5)=972(9x-5)(x-3),
由f′(x)=0,解得x=
| 5 |
| 9 |
当x∈(0,
| 5 |
| 9 |
| 5 |
| 9 |
∴当x=
| 5 |
| 9 |
| 5 |
| 9 |
因为f(x)在(0,1)上只有一个极大值,所以它是最大值,
所以当x=
| 5 |
| 9 |
点评:此题考查学生用数学解决实际问题的能力,以及运用导数求闭区间上的最值的解题思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
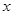 (0<
(0< ,则出厂价相应提高的比例为0.7
,则出厂价相应提高的比例为0.7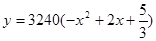 ,则当
,则当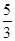 ),则当x为何值时,本年度的年利润最大?最大利润为多少?
),则当x为何值时,本年度的年利润最大?最大利润为多少?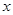 (0<
(0<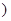 ,则出厂价相应提高的比例为0.7
,则出厂价相应提高的比例为0.7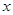 (0<
(0<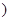 ,则出厂价相应提高的比例为0.7
,则出厂价相应提高的比例为0.7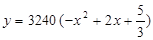 ,则当
,则当