题目内容
某汽车生产企业上年度生产一品牌汽车的投入成本为10万元/辆,出厂价为13万元/辆,年销售量为5000辆.本年度为适应市场需求,计划提高产品档次,适当增加投入成本,若每辆车投入成本增加的比例为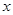 (0<
(0<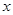 <1
<1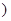 ,则出厂价相应提高的比例为0.7
,则出厂价相应提高的比例为0.7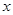 ,年销售量也相应增加.已知年利润=(每辆车的出厂价-每辆车的投入成本)×年销售量.
,年销售量也相应增加.已知年利润=(每辆车的出厂价-每辆车的投入成本)×年销售量.
(1)若年销售量增加的比例为0.4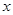 ,为使本年度的年利润比上年度有所增加,则投入成本增加的比例
,为使本年度的年利润比上年度有所增加,则投入成本增加的比例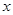 应在什么范围内?
应在什么范围内?
(2)在(1)的条件下,当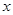 为何值时,本年度的年利润最大?最大利润为多少?
为何值时,本年度的年利润最大?最大利润为多少?
【答案】
(1) (2)
(2)  时,
时,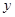 有最大值为15312.5(万元)
有最大值为15312.5(万元)
【解析】本试题主要是考查了函数在实际生活中的运用,求解了利润的最值问题。表示出函数解析式,并利用函数的单调性来解决即可。
(1)因为利润等于收入减去成本,那么先求解总的收入,以及成本,作差可以得到。由题意得:本年度每辆车的投入成本为10×(1+x);出厂价为13×(1+0.7x);年销售量为5000×(1+0.4x),
(2)在第一问的基础上可知得到利润函数是关于x的二次函数,然后根据二次函数的性质,得到最值。注意定义域的细节性。

练习册系列答案
相关题目
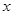 (0<
(0< ,则出厂价相应提高的比例为0.7
,则出厂价相应提高的比例为0.7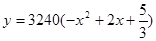 ,则当
,则当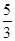 ),则当x为何值时,本年度的年利润最大?最大利润为多少?
),则当x为何值时,本年度的年利润最大?最大利润为多少?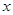 (0<
(0<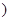 ,则出厂价相应提高的比例为0.7
,则出厂价相应提高的比例为0.7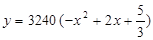 ,则当
,则当