题目内容
（本小题满分12分）设平面向量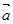
＝
（ m , 1）, 
=
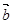( 2 , n )，其中 m， n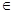 
{-2,-1,1,2}．
（I）记“使得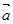⊥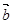成立的（
m，n ）”为事件A，求事件A发生的概率；
（II）记“使得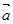//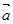（-2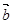）成立的（
m，n ）”为事件B，求事件B发生的概率.
【答案】
解：（I）有序数组（m,n）的所有可能结果为：（-2，-2），（-2，-1），（-2，1），（-2，2），
（-1，-2），（-1，-1），（-1，1），（-1，2），(1,-2)，（1，-1），（1，1），（1，2）,(2,-2)，
（2，-1），（2，1），（2，2）共有16种. ……………………………………3分
使得
⊥
成立的（
m，n ）,满足：2m+n=0， n=-2m
事件A有（-1，2）, (1,-2)有2种. …………………………………5分
故所求的概率为：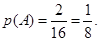
………………………………………………7分
（II）使得//（-2）成立的（
m，n ）满足：
m(1-2n)-(m-4)=0即： mn=-2 …………………………………………………9分
事件B有： （-2，1），（-1，2）,（1，-2）,（2，-1）4种 ………………………11分
故所求的概率为：
………………………………12分
【解析】略
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
