题目内容
已知直线y=2x上一点p的横坐标为a,有两个点A(-1,1)、B(3,3),使向量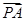 与
与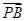 的夹角为钝角,则a的取值范围是 。
的夹角为钝角,则a的取值范围是 。
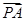 与
与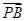 的夹角为钝角,则a的取值范围是 。
的夹角为钝角,则a的取值范围是 。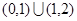
解:由题意知P点的坐标为(a,2a), PA =(-1-a,1-2a), PB =(3-a,3-2a).
由向量 PA 与 PB 的夹角为钝角,得: PA • PB =(-1-a,1-2a)•(3-a,3-2a)
=(-1-a)(3-a)+(1-2a)(3-2a)=5a2-10a<0,
∴0<a<2,但是当a=1时, PA , PB 反向共线,其夹角为π,
则向量 PA 与 PB 的夹角为钝角的充要条件是0<a<2且a≠1.
故答案为:0<a<2且a≠1.
由向量 PA 与 PB 的夹角为钝角,得: PA • PB =(-1-a,1-2a)•(3-a,3-2a)
=(-1-a)(3-a)+(1-2a)(3-2a)=5a2-10a<0,
∴0<a<2,但是当a=1时, PA , PB 反向共线,其夹角为π,
则向量 PA 与 PB 的夹角为钝角的充要条件是0<a<2且a≠1.
故答案为:0<a<2且a≠1.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
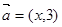 (
(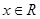 ),则“
),则“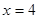 ”是“
”是“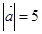 ”的( )
”的( )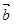 与向量
与向量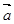 =(5,-12)的夹角是
=(5,-12)的夹角是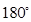 , 且
, 且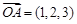 ,
,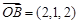 ,
,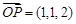 ,点Q在直线OP上运动,则当
,点Q在直线OP上运动,则当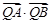 取得最小值时,点Q的坐标为( )
取得最小值时,点Q的坐标为( )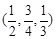
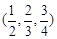
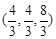
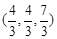
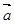 与
与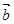 满足
满足
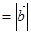 ,则( )
,则( )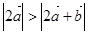
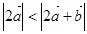
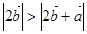
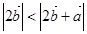
 ,且
,且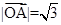 ,若点M在直线OB上(与
,若点M在直线OB上(与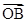 方向相同),当
方向相同),当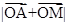 的最小值为
的最小值为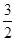 时,则
时,则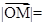 ___▲_____
___▲_____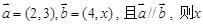 =______.
=______. ,且
,且 ,则实数
,则实数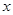 的值为 ;
的值为 ;