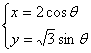Question

已知圆锥曲线C：  为参数）和定点,是此圆锥曲线的左、右焦点。

（1）以原点O为极点，以x轴的正半轴为极轴建立极坐标系，求直线的极坐标方程；

（2）经过点，且与直线垂直的直线交此圆锥曲线于两点，求的值.

 

Answer 1

【答案】

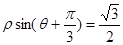(1)  (2)

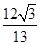
【解析】

试题分析：（1）C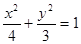：，轨迹为椭圆，其焦点,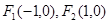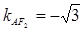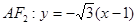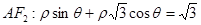

,,

即,即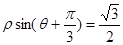

（2）由（1），

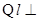
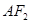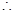
,的斜率为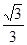，倾斜角为30⁰

所以的参数方程为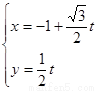（t为参数）,

代入椭圆C的方程中，得：

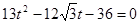
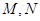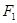因为在的异侧,

所以.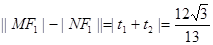

考点：本小题主要考查极坐标方程与参数方程的相关知识，考查转化推理能力.

点评：对于极坐标，要抓住极坐标与直角坐标互化公式这个关键点并灵活应用；对于参数方程，要紧紧抓住直线的参数方程、圆的参数方程、圆锥曲线的参数方程的建立以及各参数方程中参数的几何意义，同时要熟练掌握参数方程和普通方程互化的一些方法.