题目内容
为了解大学生观看某电视节目是否与性别有关,一所大学心理学教师从该校学生中随机抽取了50人进行问卷调查,得到了如下的列联表,若该教师采用分层抽样的方法从50份问卷调查中继续抽查了10份进行重点分析,知道其中喜欢看该节目的有6人
(Ⅰ) 请将上面的列联表补充完整;
(Ⅱ) 在犯错误的概率不超过0.005的情况下认为喜欢看该节目节目与性别是否有关?说明你的理由;
( III) 已知喜欢看该节目的10位男生中,A1、A2、A3、A4、A5还喜欢看新闻,B1、B2、B3还喜欢看动画片,C1、C2还喜欢看韩剧,现再从喜欢看新闻、动画片和韩剧的男生中各选出1名进行其他方面的调查,求B1和C1不全被选中的概率.
下面的临界值表供参考:
(参考公式:K2=
,其中n=a+b+c+d)
| 喜欢看该节目 | 不喜欢看该节目 | 合计 | |
| 女生 | 5 | ||
| 男生 | 10 | ||
| 合计 | 50 |
(Ⅱ) 在犯错误的概率不超过0.005的情况下认为喜欢看该节目节目与性别是否有关?说明你的理由;
( III) 已知喜欢看该节目的10位男生中,A1、A2、A3、A4、A5还喜欢看新闻,B1、B2、B3还喜欢看动画片,C1、C2还喜欢看韩剧,现再从喜欢看新闻、动画片和韩剧的男生中各选出1名进行其他方面的调查,求B1和C1不全被选中的概率.
下面的临界值表供参考:
| P(K2≥K) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
(I)由分层抽样知识知,喜欢看该节目的同学有50×
=30,故不喜欢看该节目的同学有50-30=20人,
于是可将列联表补充如下:
(Ⅱ)∵K2=
≈8.333>7.879
∴在犯错误的概率不超过0.005的情况下认为喜欢看该节目节目与性别有关.
( III)从10位男生中选出喜欢看韩剧、喜欢看新闻、喜欢看动画片的各1名,其一切可能的结果组成的基本事件如下:(A1,B1,C1),(A1,B1,C2),(A1,B2,C1),(A1,B2,C2),(A1,B3,C1),
(A1,B3,C2),(A2,B1,C1),(A2,B1,C2),(A2,B2,C1),(A2,B2,C2),(A2,B3,C1),(A2,B3,C2),(A3,B1,C1),(A3,B1,C2),(A3,B2,C1),(A3,B3,C2),(A3,B2,C2),(A3,B3,C1),(A4,B1,C1),(A4,B1,C2),(A4,B2,C1),(A4,B2,C2),(A4,B3,C1),(A4,B3,C2),(A5,B1,C1),(A5,B1,C2),(A5,B2,C1),(A5,B2,C2),(A5,B3,C1),(A5,B3,C2).
基本事件的总数为30个.
用M表示“B1、C1不全被选中”这一事件,则其对立事件
表示“B1、C1全被选中”这一事件,由于
由(A1,B1,C1),(A2,B1,C1),(A3,B1,C1),(A4,B1,C1),(A5,B1,C1),5个基本事件组成,所以P(
)=
=
,
由对立事件的概率公式得P(M)=1-P(
)=1-
=
.
| 6 |
| 10 |
于是可将列联表补充如下:
| 喜欢看该节目 | 不喜欢看该节目 | 合计 | |
| 女生 | 20 | 5 | 25 |
| 男生 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
| 50×(20×15-10×5)2 |
| 30×20×25×25 |
∴在犯错误的概率不超过0.005的情况下认为喜欢看该节目节目与性别有关.
( III)从10位男生中选出喜欢看韩剧、喜欢看新闻、喜欢看动画片的各1名,其一切可能的结果组成的基本事件如下:(A1,B1,C1),(A1,B1,C2),(A1,B2,C1),(A1,B2,C2),(A1,B3,C1),
(A1,B3,C2),(A2,B1,C1),(A2,B1,C2),(A2,B2,C1),(A2,B2,C2),(A2,B3,C1),(A2,B3,C2),(A3,B1,C1),(A3,B1,C2),(A3,B2,C1),(A3,B3,C2),(A3,B2,C2),(A3,B3,C1),(A4,B1,C1),(A4,B1,C2),(A4,B2,C1),(A4,B2,C2),(A4,B3,C1),(A4,B3,C2),(A5,B1,C1),(A5,B1,C2),(A5,B2,C1),(A5,B2,C2),(A5,B3,C1),(A5,B3,C2).
基本事件的总数为30个.
用M表示“B1、C1不全被选中”这一事件,则其对立事件
| . |
| M |
| . |
| M |
| . |
| M |
| 5 |
| 30 |
| 1 |
| 6 |
由对立事件的概率公式得P(M)=1-P(
| . |
| M |
| 1 |
| 6 |
| 5 |
| 6 |

练习册系列答案
相关题目
某报社为了解大学生对国产电影的关注程度,就“是否关注国产电影”这一问题,随机调查了某大学的60名男生和60名女生,得到如下列联表:
(1)从这60名女生中按“是否关注国产电影”采取分层抽样,抽取一个容量为6的样本,再从中随机选取2名进行深度采访,求“选到关注国产电影的女生与不关注国产电影的女生各1名”的概率;
(2)根据以上列联表,问有多大把握认为“大学生性别与关注国产电影有关”?
附:
K ,其中n=a+b+c+d为样本容量.
,其中n=a+b+c+d为样本容量.
| 男生 | 女生 | 总计 | |
| 关注国产电影 | 50 | 40 | 90 |
| 不关注国产电影 | 10 | 20 | 30 |
| 总计 | 60 | 60 | 120 |
(2)根据以上列联表,问有多大把握认为“大学生性别与关注国产电影有关”?
附:
| P(k2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
 ,其中n=a+b+c+d为样本容量.
,其中n=a+b+c+d为样本容量.
为了解大学生观看某电视节目是否与性别有关,一所大学心理学教师从该校学生中随机抽取了50人进行问卷调查,得到了如下的列联表,若该教师采用分层抽样的方法从50份问卷调查中继续抽查了10份进行重点分析,知道其中喜欢看该节目的有6人
(Ⅰ) 请将上面的列联表补充完整;
(Ⅱ) 在犯错误的概率不超过0.005的情况下认为喜欢看该节目节目与性别是否有关?说明你的理由;
( III) 已知喜欢看该节目的10位男生中,A1、A2、A3、A4、A5还喜欢看新闻,B1、B2、B3还喜欢看动画片,C1、C2还喜欢看韩剧,现再从喜欢看新闻、动画片和韩剧的男生中各选出1名进行其他方面的调查,求B1和C1不全被选中的概率.
下面的临界值表供参考:
(参考公式: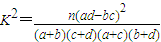 ,其中n=a+b+c+d)
,其中n=a+b+c+d)
| 喜欢看该节目 | 不喜欢看该节目 | 合计 | |
| 女生 | 5 | ||
| 男生 | 10 | ||
| 合计 | 50 |
(Ⅱ) 在犯错误的概率不超过0.005的情况下认为喜欢看该节目节目与性别是否有关?说明你的理由;
( III) 已知喜欢看该节目的10位男生中,A1、A2、A3、A4、A5还喜欢看新闻,B1、B2、B3还喜欢看动画片,C1、C2还喜欢看韩剧,现再从喜欢看新闻、动画片和韩剧的男生中各选出1名进行其他方面的调查,求B1和C1不全被选中的概率.
下面的临界值表供参考:
| P(K2≥K) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
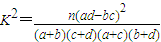 ,其中n=a+b+c+d)
,其中n=a+b+c+d)