题目内容
(2007•武汉模拟)在一个单位中普查某种疾病,600个人去验血,对这些人的血的化验可以用两种方法进行:
方法一:每个人的血分别化验,这时需要化验600次;
方法二:把每个人的血样分成两份,取k(k≥2)个人的血样各一份混在一起进行化验,如果结果是阴性的,那么对这k个人只作一次检验就够了;如果结果阳性的,那么再对这k个人的另一份血样逐个化验,这时对这k个人共需作k+1次化验.
假定对所有的人来说,化验结果是阳性的概率是0.1,而且这些人的反应是独立的.将每个人的血样所需的检验次数作为随机变量ξ.
(1)写出方法二中随机变量ξ的分布列,并求数学期望Eξ(用k表示);
(2)现有方法一和方法二中k分别取3、4、5共四种方案,请判断哪种方案最好,并说明理由.(参考数据:取0.93=0.729,0.94=0.656,0.95=0.591)
方法一:每个人的血分别化验,这时需要化验600次;
方法二:把每个人的血样分成两份,取k(k≥2)个人的血样各一份混在一起进行化验,如果结果是阴性的,那么对这k个人只作一次检验就够了;如果结果阳性的,那么再对这k个人的另一份血样逐个化验,这时对这k个人共需作k+1次化验.
假定对所有的人来说,化验结果是阳性的概率是0.1,而且这些人的反应是独立的.将每个人的血样所需的检验次数作为随机变量ξ.
(1)写出方法二中随机变量ξ的分布列,并求数学期望Eξ(用k表示);
(2)现有方法一和方法二中k分别取3、4、5共四种方案,请判断哪种方案最好,并说明理由.(参考数据:取0.93=0.729,0.94=0.656,0.95=0.591)
分析:(1)对于方法二,当k个人一组的混合血液呈阴性时,可以认为每个人需要化验的次数为
次;当k个人一组的混合血液呈阳性时,可以认为每个人需要化验的次验为
+1次,然后分别求出相应的概率,利用数学期望公式解之即可;
(2)对方法一:P(ξ=1)=1 Eξ=1,然后计算出方法二中k分别取3、4、5时的数学期望,比较四种方案即可判定哪种方案最好.
| 1 |
| k |
| 1 |
| k |
(2)对方法一:P(ξ=1)=1 Eξ=1,然后计算出方法二中k分别取3、4、5时的数学期望,比较四种方案即可判定哪种方案最好.
解答:解:(1)对于方法二,k个人一组的混合血液呈阴性结果的概率为0.9k,呈阳性结果的概率为1-0.9k.
当k个人一组的混合血液呈阴性时,可以认为每个人需要化验的次数为
次;当k个人一组的混合血液呈阳性时,可以认为每个人需要化验的次验为
+1次.
所以(3分)
∴Eξ=
×0.9k+(1+
)(1-0.9k)=1+
-0.9k.(5分)
(2)对方法一:P(ξ=1)=1 Eξ=1.(6分)
当k=3时,Eξ=1+
-0.93≈0.604;
当k=4时,Eξ=1+
-0.94≈0.597;
当k=5时,Eξ=1+
-0.95≈0.609.(9分)
比较知k=4时的方案最好(10分)
当k个人一组的混合血液呈阴性时,可以认为每个人需要化验的次数为
| 1 |
| k |
| 1 |
| k |
所以(3分)
| ξ |
|
1+
| ||||
| P | 0.9k | 1-0.9k |
| 1 |
| k |
| 1 |
| k |
| 1 |
| k |
(2)对方法一:P(ξ=1)=1 Eξ=1.(6分)
当k=3时,Eξ=1+
| 1 |
| 3 |
当k=4时,Eξ=1+
| 1 |
| 4 |
当k=5时,Eξ=1+
| 1 |
| 5 |
比较知k=4时的方案最好(10分)
点评:本题主要考查了数列的应用,同时考查了离散型变量的数学期望以及计算能力,属于中档题.

练习册系列答案
相关题目
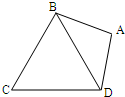 (2007•武汉模拟)如图,在平面四边形ABCD中,AB=AD=1,∠BAD=θ,而△BCD是正三角形,
(2007•武汉模拟)如图,在平面四边形ABCD中,AB=AD=1,∠BAD=θ,而△BCD是正三角形, (2007•武汉模拟)如图,直线l:y=
(2007•武汉模拟)如图,直线l:y=