题目内容
下列函数中,在区间 上为增函数的是
上为增函数的是
A. | B. |
C.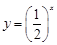 | D.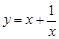 |
A
解析试题分析: 因为选项A中,现看定义域x>-2,且是一个复合函数,内层是一次递增函数,外层是递增的自然对数函数y=lnx,那么利用同增异减来判定,选项A成立。
选项B中,由于定义域x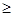 -1,同时因为y=
-1,同时因为y=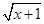 是递增函数,那么则可知
是递增函数,那么则可知 是递减函数。错误
是递减函数。错误
选项C中,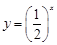 表示的为底数小于1的指数函数,因此是单调递减函数,错误。而选项D中,由于
表示的为底数小于1的指数函数,因此是单调递减函数,错误。而选项D中,由于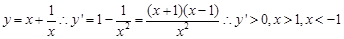 ,可见增区间为x>1,故错误,选A.
,可见增区间为x>1,故错误,选A.
考点:本题主要考查了函数单调性的运用以及判定问题。
点评:解决该试题的关键是能利用对数函数与指数函数单调性的底数的范围来确定处增减性,同时能根据导数的思想来证明对勾函数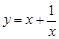 的单调性。
的单调性。

练习册系列答案
相关题目
定义新运算“&”与“ ”:
”: ,
, ,则函数
,则函数
是( )
| A.奇函数 | B.偶函数 |
| C.非奇非偶函数 | D.既是奇函数又是偶函数 |
若函数y=ax+b-1(a>0且a≠1 )的图象经过一、三、四象限,则下列结论中正确的是( )
| A.a>1且b<1 | B.0<a<1 且b<0 |
| C.0<a<1 且b>0 | D.a>1 且b<0 |
设 为实数,则
为实数,则 与
与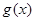 表示同一个函数的是 ( )
表示同一个函数的是 ( )
A. | B.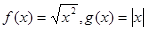 |
C.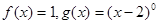 | D. |
已知函数 在
在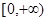 上是增函数,
上是增函数, ,若
,若 ,则
,则 的取值范围是( )
的取值范围是( )
A. | B.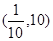 |
C. | D. |
设方程 的实根为
的实根为 ,方程
,方程 的实根为
的实根为 ,函数
,函数 则
则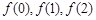 的大小关系是( )
的大小关系是( )
A. | B. |
C. | D. |
已知 上是增函数,那么实数a的取值范围是( )
上是增函数,那么实数a的取值范围是( )
A.(1,+ ) ) | B.( ) ) | C. | D.(1,3) |
已知函数 满足
满足 ,且
,且 是偶函数,当
是偶函数,当 时,
时, ,若在区间
,若在区间 内,函数
内,函数 有
有 个零点,则实数
个零点,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
设函数f(x)= +lnx 则 ( )
+lnx 则 ( )
A.x= 为f(x)的极大值点 为f(x)的极大值点 | B.x= 为f(x)的极小值点 为f(x)的极小值点 |
| C.x=2为 f(x)的极大值点 | D.x=2为 f(x)的极小值点 |