题目内容
【题目】对于实数a,b,定义运算“*”:a*b=![]() ,设f (x)=(x-4)*
,设f (x)=(x-4)*![]() ,若关于x的方程|f (x)-m|=1(m∈R)恰有四个互不相等的实数根,则实数m的取值范围是________.
,若关于x的方程|f (x)-m|=1(m∈R)恰有四个互不相等的实数根,则实数m的取值范围是________.
【答案】(-1,1)∪(2,4)
【解析】
根据新定义得出f(x)的解析式,作出f(x)的函数图象,则f(x)与y=m±1共有4个交点,根据图象列出不等式组解出.
解不等式x﹣4≤![]() ﹣4得x≥0,f(x)=
﹣4得x≥0,f(x)=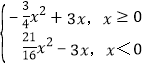 ,
,
画出函数f(x)的大致图象如图所示.
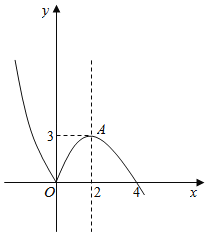
因为关于x的方程|f(x)﹣m|=1(m∈R),即f(x)=m±1(m∈R)恰有四个互不相等的实数根,
所以两直线y=m±1(m∈R)与曲线y=f(x)共有四个不同的交点,
∴![]() 或
或![]() 或
或![]() ,
,
解得2<m<4或﹣1<m<1.
故答案为(﹣1,1)∪(2,4).

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
【题目】已知某单位甲、乙、丙三个部门共有员工60人,为调查他们的睡眠情况,通过分层抽样获得部分员工每天睡眠的时间,数据如下表(单位:小时)
甲部门 | 6 | 7 | 8 | |||
乙部门 | 5.5 | 6 | 6.5 | 7 | 7.5 | 8 |
丙部门 | 5 | 5.5 | 6 | 6.5 | 7 | 8.5 |
(1)求该单位乙部门的员工人数?
(2)从甲部门和乙部门抽出的员工中,各随机选取一人,甲部门选出的员工记为A,乙部门选出的员工记为B,假设所有员工睡眠的时间相互独立,求A的睡眠时间不少于B的睡眠时间的概率;
(3)若将每天睡眠时间不少于7小时视为睡眠充足,现从丙部门抽出的员工中随机抽取3人做进一步的身体检查.用X表示抽取的3人中睡眠充足的员工人数,求随机变量X的分布列与数学期望.

