题目内容
15.设数列{an}满足a1=1,a1+a2+…+an-1=an-1(n≥2,n∈N*).(1)求数列{an}的通项公式;
(2)若数列{an}满足logabn=an(a>1),求证:$\frac{a}{{a}^{2}-1}$≤$\frac{{b}_{1}}{{b}_{2}-1}$+$\frac{{b}_{2}}{{b}_{3}-1}$+…+$\frac{{b}_{n-1}}{{b}_{n}-1}$$<\frac{1}{a-1}$.
分析 (1)将表达式a1+a2+…+an-1=an-1(n≥2,n∈N*)两边都加上an,得Sn=2an-1,从而an=Sn-Sn-1=2an-2an-1,即得通项公式;
(2)确定)bn=${a}^{{2}^{n-1}}$,化简$\frac{{b}_{1}}{{b}_{2}-1}$+$\frac{{b}_{2}}{{b}_{3}-1}$+…+$\frac{{b}_{n-1}}{{b}_{n}-1}$=$\frac{1}{a-1}$-$\frac{1}{{a}^{{2}^{n-1}}-1}$.即可证明结论.
解答 解:(1)∵a1+a2+…+an-1=an-1(n≥2,n∈N*),
∴a1+a2+…+an-1+an=2an-1,即Sn=2an-1,
∴an=Sn-Sn-1=2an-1-(2an-1-1)=2an-2an-1,
即an=2an-1,又a1=1,
∴an=1×2n-1=2n-1;
(2)数列{an}满足logabn=an(a>1),∴bn=${a}^{{2}^{n-1}}$,
∴$\frac{{b}_{k-1}}{{b}_{k}-1}$=$\frac{1}{{a}^{{2}^{k-2}}-1}$-$\frac{1}{{a}^{{2}^{k-1}}-1}$,
∴$\frac{{b}_{1}}{{b}_{2}-1}$+$\frac{{b}_{2}}{{b}_{3}-1}$+…+$\frac{{b}_{n-1}}{{b}_{n}-1}$=$\frac{1}{a-1}$-$\frac{1}{{a}^{{2}^{n-1}}-1}$,
∵{$\frac{1}{a-1}$-$\frac{1}{{a}^{{2}^{n-1}}-1}$}是一个递增数列,
∴$\frac{1}{{a}^{{2}^{n-1}}-1}$>0,$\frac{1}{a-1}$-$\frac{1}{{a}^{{2}^{n-1}}-1}$≥$\frac{1}{a-1}$-$\frac{1}{{a}^{{2}^{2-1}}-1}$=$\frac{a}{{a}^{2}-1}$,
∴$\frac{a}{{a}^{2}-1}$≤$\frac{1}{a-1}$-$\frac{1}{{a}^{{2}^{n-1}}-1}$<$\frac{1}{a-1}$,
∴$\frac{a}{{a}^{2}-1}$≤$\frac{{b}_{1}}{{b}_{2}-1}$+$\frac{{b}_{2}}{{b}_{3}-1}$+…+$\frac{{b}_{n-1}}{{b}_{n}-1}$$<\frac{1}{a-1}$.
点评 本题考查数列的通项公式,递推公式,对表达式的灵活变形是解题的关键,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 4 | B. | 3$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 8 |
| A. | 假设n=k(k∈N)时命题成立,即xk+yk能被x+y整除 | |
| B. | 假设n≥k(k∈N)时命题成立,即xk+yk能被x+y整除 | |
| C. | 假设n=2k+1(k∈N*)时命题成立,即x2k+1+y2k+1能被x+y整除 | |
| D. | 假设n=2k-1(k∈N*)时命题成立,即x2k-1+y2k-1能被x+y整除 |
 如图,在平面直角坐标系xOy中,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左右焦点分别为,F1和F2,上顶点为B,BF2,延长线交椭圆于点A,△ABF的周长为8,且$\overrightarrow{B{F_1}}•\overrightarrow{BA}$=0.
如图,在平面直角坐标系xOy中,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左右焦点分别为,F1和F2,上顶点为B,BF2,延长线交椭圆于点A,△ABF的周长为8,且$\overrightarrow{B{F_1}}•\overrightarrow{BA}$=0.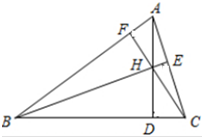 如图,已知△ABC的三条高是AD,BE,CF,用向量方法证明:AD,BE,CF相交于一点.
如图,已知△ABC的三条高是AD,BE,CF,用向量方法证明:AD,BE,CF相交于一点. 如图,在正四棱台ABCD-A1B1C1D1中,A1B1=a,AB=2a,AA1=$\sqrt{2}a$,E,F分别是AD,AB的中点.
如图,在正四棱台ABCD-A1B1C1D1中,A1B1=a,AB=2a,AA1=$\sqrt{2}a$,E,F分别是AD,AB的中点.