题目内容
设函数![]() 的图象在点
的图象在点![]() 处的切线的斜率为
处的切线的斜率为![]() ,且函数
,且函数![]() 为偶函数.若函数
为偶函数.若函数![]() 满足下列条件:①
满足下列条件:①![]() ;②对一切实数
;②对一切实数![]() ,不等式
,不等式![]() 恒成立.
恒成立.
(Ⅰ)求函数![]() 的表达式;
的表达式;
(Ⅱ)求证:![]()
![]() .
.
(Ⅰ)解:由已知得:![]() . ……………1分
. ……………1分
由![]() 为偶函数,得
为偶函数,得![]() 为偶函数,
为偶函数,
显然有![]() . …………2分
. …………2分
又![]() ,所以
,所以![]() ,即
,即![]() . …………3分
. …………3分
又因为![]() 对一切实数
对一切实数![]() 恒成立,
恒成立,
即对一切实数![]() ,不等式
,不等式![]() 恒成立. …………4分
恒成立. …………4分
显然,当![]() 时,不符合题意. …………5分
时,不符合题意. …………5分
当![]() 时,应满足
时,应满足
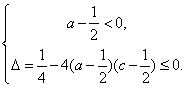
注意到![]() ,解得
,解得![]() . …………7分
. …………7分
所以![]() . ……………8分
. ……………8分
(Ⅱ)证明:因为![]() ,所以
,所以![]() .………9分
.………9分
要证不等式![]() 成立,
成立,
即证![]() . …………10分
. …………10分
因为![]() , …………12分
, …………12分
所以![]()
![]() .
.
所以![]() 成立. ……………14分
成立. ……………14分

练习册系列答案
相关题目
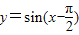 在[0,π]上是减函数;
在[0,π]上是减函数;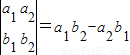 则函数
则函数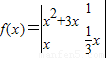 的图象在点
的图象在点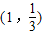 处的切线方程是6x-3y-5=0.
处的切线方程是6x-3y-5=0. 在[0,π]上是减函数;
在[0,π]上是减函数;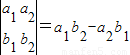 则函数
则函数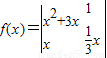 的图象在点
的图象在点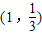 处的切线方程是6x-3y-5=0.
处的切线方程是6x-3y-5=0.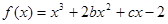 的图象在点
的图象在点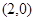 处的切线方程是
处的切线方程是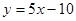 .
.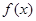 的解析式;
的解析式; 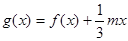 ,若
,若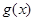 的极值存在,求实数
的极值存在,求实数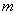 的取值范围
的取值范围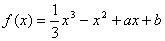 的图象在点
的图象在点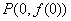 处的切线方程为
处的切线方程为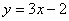
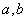 的值;
的值;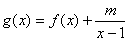 是[2,+∞)上的增函数。
是[2,+∞)上的增函数。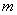 的最大值;
的最大值;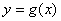 围成两个封闭图形,则这两个封闭图形的面积总相等?若存在,求出点Q的坐标;若不存在,说明理由。
围成两个封闭图形,则这两个封闭图形的面积总相等?若存在,求出点Q的坐标;若不存在,说明理由。