题目内容
知函数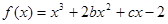 的图象在点
的图象在点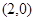 处的切线方程是
处的切线方程是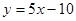 .
.
(1)求函数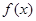 的解析式;
的解析式;
(2)设函数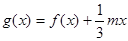 ,若
,若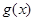 的极值存在,求实数
的极值存在,求实数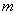 的取值范围
的取值范围
【答案】
【解】:(I)由已知,切点为(2,0),故有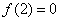 ,即
,即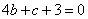 ……①
……①
又 ,由已知
,由已知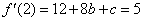 得
得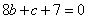 ……②
……②
联立①②,解得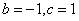 .
.
所以函数的解析式为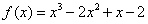
(II)因为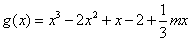 令
令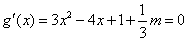
当函数有极值时,则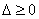 ,方程
,方程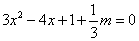 有实数解,
有实数解,
由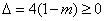 ,得
,得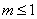 .
.
①当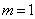 时,
时,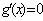 有实数
有实数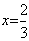 ,在
,在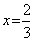 左右两侧均
左右两侧均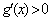 ,故函数
,故函数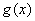 无极值
无极值
②当 时,
时,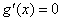 有两个实数根
有两个实数根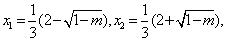
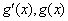 情况如下表:
情况如下表:
|
|
|
|
|
|
|
|
|
+ |
0 |
- |
0 |
+ |
|
|
↗ |
极大值 |
↘ |
极小值 |
↗ |
所以在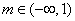 时,函数
时,函数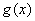 有极值.
有极值.
【解析】略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
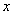

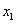
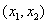
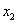
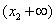
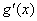
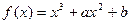 的图象在点
的图象在点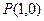 处的切线与直线
处的切线与直线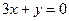 平行.
平行. 的解析式;
的解析式;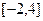 上的最小值和最大值.
上的最小值和最大值.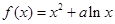 的图象在点
的图象在点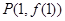 处的切线斜率为
处的切线斜率为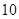 .
.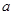 的值;
的值;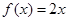 根的个数,证明你的结论;
根的个数,证明你的结论;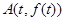 ,使得曲线
,使得曲线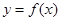 在该点附近的左、右的两部分分别位于曲线在该点处切线的两侧?若存在,求出点A的坐标;若不存在,说明理由.
在该点附近的左、右的两部分分别位于曲线在该点处切线的两侧?若存在,求出点A的坐标;若不存在,说明理由. 的图象在点
的图象在点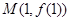 处的切线方程为
处的切线方程为 。
。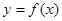 的解析式;
的解析式;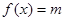 在区间
在区间 上恰有两个相异实根,求m的取值范围。
上恰有两个相异实根,求m的取值范围。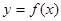 的图象在点
的图象在点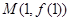 处的切线方程是
处的切线方程是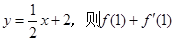 = 。
= 。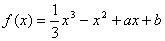 的图象在点
的图象在点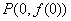 处的切线方程为
处的切线方程为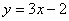
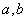 的值;
的值;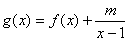 是[2,+∞)上的增函数。
是[2,+∞)上的增函数。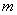 的最大值;
的最大值;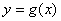 围成两个封闭图形,则这两个封闭图形的面积总相等?若存在,求出点Q的坐标;若不存在,说明理由。
围成两个封闭图形,则这两个封闭图形的面积总相等?若存在,求出点Q的坐标;若不存在,说明理由。