题目内容
在二项式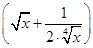 n的展开式中,前三项的系数成等差数列,把展开式中所有的项重新排成一列,有理项都互不相邻的概率为( )
n的展开式中,前三项的系数成等差数列,把展开式中所有的项重新排成一列,有理项都互不相邻的概率为( )
A.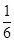 B.
B.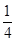
C.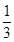 D.
D.
【答案】
D
【解析】注意到二项式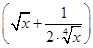 n的展开式的通项是Tr+1=Cnr·(
n的展开式的通项是Tr+1=Cnr·(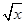 )n-r·
)n-r·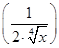 r=Cnr·2-r·x
r=Cnr·2-r·x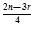 .依题意有Cn0+Cn2·2-2=2Cn1·2-1=n,即n2-9n+8=0,(n-1)(n-8)=0(n≥2),因此n=8 .∵二项式
.依题意有Cn0+Cn2·2-2=2Cn1·2-1=n,即n2-9n+8=0,(n-1)(n-8)=0(n≥2),因此n=8 .∵二项式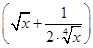 8的展开式的通项是Tr+1=C8r·2-r·x
8的展开式的通项是Tr+1=C8r·2-r·x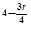 ,其展开式中的有理项共有3项,所求的概率等于
,其展开式中的有理项共有3项,所求的概率等于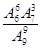 =
=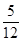 .
.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
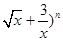 的展开式中,各项系数之和为M,各项二项式系数之和为N,且M+N=72,则展开式中常数项的值为
的展开式中,各项系数之和为M,各项二项式系数之和为N,且M+N=72,则展开式中常数项的值为