Question

若函数y=f（x）（x∈R）满足f（x-2）=f（x），且x∈[-1，1]时，f（x）=1-x²，函数g（x）=

lgx(x＞0) - 1 x (x＜0)

，则函数h（x）=f（x）-g（x）在区间[-5，6]内的零点有

9

个．

Answer 1

分析：在同一坐标系内分别画出函数y=f（x）、y=lgx、y=-

1

x

的图象，其交点的个数即为函数h（x）的零点的个数．

解答：解：∵函数y=f（x）（x∈R）满足f（x-2）=f（x），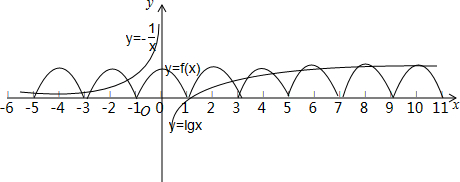
∴函数f（x）周期为2 的函数，
先画出x∈[-1，1]时，
f（x）=1-x²的图象，进而可画出[-5，6]区间上的图象．
在同一坐标系内画出函数
g（x）的图象，
由图象可以看出：
函数y=f（x）与y=g（x）在区间[-5，6]内的交点共有 9个，即函数h（x）=f（x）-g（x）在区间[-5，6]内的零点有 9个．
故答案为9．

点评：根据函数解析式正确画出函数图象是解题的关键．