题目内容
(1)已知α,β为锐角,且cosα=
,cos(α+β)=-
,求β;
(2)已知tan(
+α)=
,求
的值.
| 1 |
| 7 |
| 11 |
| 14 |
(2)已知tan(
| π |
| 4 |
| 1 |
| 2 |
| sin2α-cos2α |
| 1+cos2α |
分析:(1)由已知利用同角基本关系可求sinα,sin(α+β),利用sinβ=sin[(α+β)-α]=sin(α+β)cosα-sinαcos(α+β)可求sinβ,进而可求
(2)由tan(
+α)=
,结合两角和的正切公式可求tanα,然后把所求式子利用二倍角公式进行化简代人可求
(2)由tan(
| π |
| 4 |
| 1 |
| 2 |
解答:解:(1)∵α,β为锐角,且cosα=
,cos(α+β)=-
,
∴sinα=
=
,sin(α+β)=
=
∴sinβ=sin[(α+β)-α]=sin(α+β)cosα-sinαcos(α+β)
=
×
-
×(-
)
=
∴β=60°
(2)∵tan(
+α)=
,
∴
=
∴tanα=-
∴
=
=
=2tanα-
=-
| 1 |
| 7 |
| 11 |
| 14 |
∴sinα=
1-
|
4
| ||
| 7 |
1-(-
|
5
| ||
| 14 |
∴sinβ=sin[(α+β)-α]=sin(α+β)cosα-sinαcos(α+β)
=
5
| ||
| 14 |
| 1 |
| 7 |
4
| ||
| 7 |
| 11 |
| 14 |
=
| ||
| 2 |
∴β=60°
(2)∵tan(
| π |
| 4 |
| 1 |
| 2 |
∴
| 1+tanα |
| 1-tanα |
| 1 |
| 2 |
∴tanα=-
| 1 |
| 3 |
∴
| sin2α-cos2α |
| 1+cos2α |
| 2sinαcosα-cos2α |
| 2cos2α |
| 2sinα-cosα |
| 2cosα |
=2tanα-
| 1 |
| 2 |
| 7 |
| 6 |
点评:本题主要考查了同角平方关系,和差角公式及二倍角公式的综合应用,解题的关键是熟练掌握基本公式

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 是棱长为
是棱长为 的正方体,点
的正方体,点 在
在 上,点
上,点 在
在 上,且
上,且 .
. 四点共面;(4分)
四点共面;(4分) 在
在 上,
上,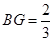 ,点
,点 在
在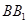 上,
上, ,垂足为
,垂足为 ,求证:
,求证: 平面
平面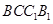 ;(4分)
;(4分) 表示截面
表示截面 和侧面
和侧面 .(4分
.(4分
 的正方体
的正方体 中,
中, 为棱
为棱 的中点,
的中点, 为正方形
为正方形 的中心,点
的中心,点 分别在直线
分别在直线 和
和 上.
上.
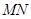 与
与 所成角的余弦值;
所成角的余弦值; 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.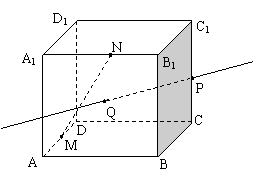 (本题满分16分)已知在棱长为
(本题满分16分)已知在棱长为 (本题满分16分)已知在棱长为
(本题满分16分)已知在棱长为