题目内容
(本小题14分)四棱锥![]() 中,底面
中,底面![]() 为矩形,侧面
为矩形,侧面![]() 底面
底面![]() ,
,![]()
![]() .
.
(I)取![]() 的中点为
的中点为![]() ,
,![]() 的中点为
的中点为![]() ,证明:FG∥面
,证明:FG∥面![]() ;
;
 (II)证明:
(II)证明:![]() .
.
解答
(I)证明:取AB中点H,连接GH,CH
因为G是AE中点,所以HG∥=![]() BE,又因为矩形BCDE,所以BE∥=CD,且F是CD中点,
BE,又因为矩形BCDE,所以BE∥=CD,且F是CD中点,
所以HG∥=CF,所以四边形FGHC是平行四边形,所以FG∥CH,………………………………4分
又因为FG![]() 平面ABC,CH
平面ABC,CH![]() 平面ABC,所以FG∥面
平面ABC,所以FG∥面![]() ;………………………………7分
;………………………………7分
(II)取BC中点Q,连接AQ,DQ
因为AC=AB,所以AQ⊥BC,
因为侧面![]() 底面
底面![]() ,AQ
,AQ![]() 平面ABC,平面ABC∩平面
平面ABC,平面ABC∩平面![]() =BC,
=BC,
所以AQ⊥平面BCDE,……………………………………………………………………………………8分
因为CE![]() 平面BCD ,所以 CE⊥AQ……………………………………………………………9分
平面BCD ,所以 CE⊥AQ……………………………………………………………9分
又在矩形BCDE中,![]() ,BE=
,BE=![]() ,CQ=1, 所以
,CQ=1, 所以![]()
所以Rt△CDQ∽Rt△BCE,所以∠DQC=∠CEB, ………………………………………………10分
所以∠DQC+∠BCE=∠CEB+∠BCE=90o ,所以CE⊥BQ…………………………12分(其他方法参照给分)
因为AQ∩BQ=Q,所以CE⊥平面ADQ,………………………………………………13分
AD![]() 平面ADQ,所以
平面ADQ,所以![]() ………………………………………………………………14分
………………………………………………………………14分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

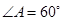 、边长为
、边长为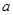 的菱形,又
的菱形,又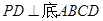 ,且PD=CD,点M、N分别是棱AD、PC的中点.
,且PD=CD,点M、N分别是棱AD、PC的中点.
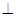 平面PAD;
平面PAD;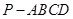 中,底面
中,底面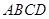 为矩形,侧棱
为矩形,侧棱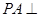 底面
底面 为
为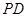 的中点.
的中点.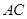 与
与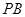 所成角的余弦值;
所成角的余弦值;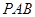 内找一点
内找一点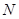 ,使
,使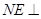 平面
平面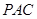 ,并分别求出点
,并分别求出点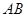 和
和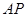 的距离.
的距离.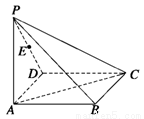
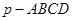 中,侧面
中,侧面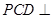 底面
底面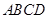 ,
,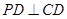 ,
,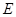 为
为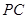 中点,底面
中点,底面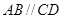 ,
,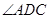 =90°,
=90°,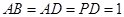 ,
,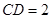 。
。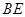
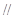 平面
平面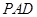 ;
;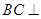 平面
平面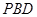 ;
;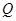 为侧棱
为侧棱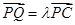 ,试确定
,试确定 的值,使得二面角
的值,使得二面角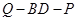 为45°。
为45°。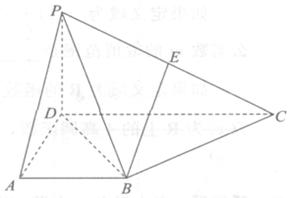
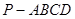 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱 底面ABCD,
底面ABCD, ,E是PC的中点,作
,E是PC的中点,作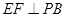 交PB于点F.
交PB于点F.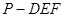 的体积.
的体积.