题目内容
（本小题14分）已知四棱锥P-ABCD，底面ABCD是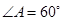
、边长为
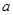的菱形，又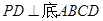
，且PD=CD，点M、N分别是棱AD、PC的中点．
（1）证明：DN//平面PMB；
（2）证明：平面PMB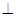
平面PAD；
（3）求点A到平面PMB的距离．
【答案】
解：（1）证明：取PB中点Q，连结MQ、NQ，
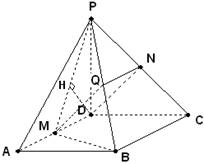
因为M、N分别是棱AD、PC中点，所以
QN//BC//MD，且QN=MD，于是DN//MQ.
.…
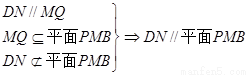…………………6分
（2）
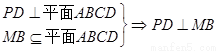
又因为底面ABCD是
、边长为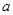
的菱形，且M为AD中点，
所以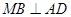
.又
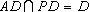所以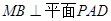
.
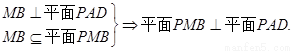………………10分
（3）因为M是AD中点，所以点A与D到平面PMB等距离.
过点D作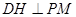
于H，由（2）平面PMB
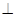平面PAD，所以
.
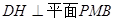故DH是点D到平面PMB的距离.
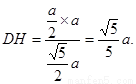所以点A到平面PMB的距离为
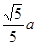.………14分
【解析】略
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
点
，过
点作圆
的切线
为切点．
所在直线的方程；
；
的方程．
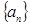满足
，且
是
，
的等差中项.
，
，求使 
成立的正整数
的最小值.
，设
。
图象上任意一点
为切点的切线的斜率
恒成立，求实数
的最小值。
，使得函数
的图象与
的图象恰好有四个不同的交点？若存在，求出
的图像与函数
的图像关于点
对称
，
在区间
上的值不小于6，求实数a的取值范围．
的图像在[a,b]上连续不断，定义：
，
，其中
表示函数
在D上的最小值，
表示函数
对任意的
成立，则称函数
上的“k阶收缩函数”
，试写出
，
的表达式；
试判断
，函数
是[0,b]上的2阶收缩函数，求b的取值范围