题目内容
6.某企业生产一种产品,其成本为每件16元,经调研,该产品以20元一件投放市场,每年能销售360件,若产品以25元/件投放市场,每年能销售210件,假定年销售件数y是价格x元/件的一次函数.(1)试求y与x之间的关系式.
(2)在企业不积压且不考虑其他因素的条件下,问销售价格定为多少时,才能使每年获得最大利润?每年的最大利润是多少?(总利润=销售总收入-总成本)
分析 (1)设y=kx+b,利用待定系数法求出k,b,即可求y与x之间的关系式.
(2)求出利润函数,利用一元二次函数的性质求出最值即可得到结论.
解答 解:(1)设y=kx+b,则由题意得$\left\{\begin{array}{l}{20k+b=360}\\{25k+b=210}\end{array}\right.$,
解得k=-30,b=960,则y与x之间的关系式为y=-30x+960,(16≤x≤32).
(2)每月获得利润P=(-30x+960)(x-16)=-30x2+1440x-512×30=-30(x-24)2+1920,
∴当x=24时,函数取得最大值,此时最大值为1920.
点评 本题主要考查函数的应用问题,利用待定系数法求出函数的解析式以及结合一元二次函数的性质是解决本题的关键.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
15.钝角三角形ABC的面积是1,AB=2,$BC=\sqrt{2}$,则AC=( )
| A. | 2 | B. | $\sqrt{2}$ | C. | 10 | D. | $\sqrt{10}$ |
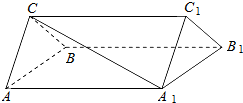 如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°,E为BC中点
如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°,E为BC中点