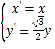题目内容
【题目】对于正整数
，若存在1，2，…，的一个排列
满足
（
），则称为“循球数”.证明：
（1）9、11都是循环数；
（2）为循环数的一个必要不充分条件是
为质数.
【答案】（1）见解析（2）见解析
【解析】
（1）易知，“1，2，4，8，3，6，7，5，9”和“1，2，4，8，7，9，5，10，3，6，11”分别是“1，2，…，9”和“1，2，…，11”的满足循环数定义的排列.故9、11都是循环数.
（2）若
不是质数，由
，知存在质数
和奇数
，使得
.
若
为循环数，“
”是“1，2，…，”的一个排列，满足循环数定义，由循环性，不妨设
，于是，
，…，存在
，使得
，
，
，或
.
显然，每项都具有“
的整数倍加或减2的整数次幂”的形式.
由和，得
.
从而，
.
故
.
因此，为质数是为循环数的必要条件.
由
是质数，易知，8不是循环数.
练习册系列答案
相关题目
【题目】某市的教育主管部门对所管辖的学校进行年终督导评估，为了解某学校师生对学校教学管理的满意度，分别从教师和不同年级的同学中随机抽取若干师生，进行评分(满分100分)，绘制如下频率分布直方图(分组区间为
， 
， 
， 
， 
， 
)，并将分数从低到高分为四个等级：
满意度评分 |
|
|
|
|
满意度等级 | 不满意 | 基本满意 | 满意 | 非常满意 |
已知满意度等级为基本满意的有340人.
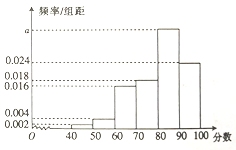
(1)求表中
的值及不满意的人数；
(2)在等级为不满意的师生中，老师占
，现从该等级师生中按分层抽样抽取12人了解不满意的原因，并从中抽取3人担任整改督导员，记
为老师整改督导员的人数，求
的分布列及数学期望.
