题目内容
4.设f(x)是R上的函数,满足|f(x)+cos2x|≤$\frac{3}{4}$,|f(x)-sin2x|≤$\frac{1}{4}$,则f(x)=$\frac{3}{4}$-cos2x.分析 先解绝对值不等式得到:$\left\{\begin{array}{l}{-\frac{3}{4}-co{s}^{2}x≤f(x)≤\frac{3}{4}-co{s}^{2}x}\\{-\frac{1}{4}+si{n}^{2}x≤f(x)≤\frac{1}{4}+si{n}^{2}x}\end{array}\right.$,通过求f(x)的范围,便可得到$-\frac{1}{4}+si{n}^{2}x≤f(x)≤\frac{3}{4}-co{s}^{2}x$,这样便可得到f(x)=$\frac{3}{4}-co{s}^{2}x$.
解答 解:根据条件:$\left\{\begin{array}{l}{-\frac{3}{4}≤-\frac{3}{4}-co{s}^{2}x≤f(x)≤\frac{3}{4}-co{s}^{2}x≤\frac{3}{4}}\\{-\frac{1}{4}≤-\frac{1}{4}+si{n}^{2}x≤f(x)≤\frac{1}{4}+si{n}^{2}x≤\frac{5}{4}}\end{array}\right.$;
∴$-\frac{1}{4}+si{n}^{2}x≤f(x)≤\frac{3}{4}-co{s}^{2}x$;
∴$\frac{3}{4}-co{s}^{2}x≤f(x)≤\frac{3}{4}-co{s}^{2}x$;
∴$f(x)=\frac{3}{4}-co{s}^{2}x$.
故答案为:$\frac{3}{4}-co{s}^{2}x$.
点评 考查绝对值不等式的解法,sin2x+cos2x=1,以及sin2x,cos2x的取值范围.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
12.圆x2+y2-4x+6y=0截x轴与截y轴所得的弦长之比为( )
| A. | $\frac{4}{9}$ | B. | $\frac{9}{4}$ | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |
19.已知α,β满足1+cosα-sinβ+sinαsinβ=0,1-cosα-cosβ+sinαcosβ=0,则sinα的值为( )
| A. | $\frac{1-\sqrt{10}}{3}$ | B. | $\frac{\sqrt{10}-1}{3}$ | C. | $\frac{1+\sqrt{10}}{7}$ | D. | -$\frac{1+\sqrt{10}}{3}$ |
16.要把5本不同的故事书和6本不同的科技书放在书架上排成一排,其中同类书恰好排在一起的概率是( )
| A. | $\frac{2}{231}$ | B. | $\frac{1}{231}$ | C. | $\frac{2}{11}$ | D. | $\frac{1}{11}$ |
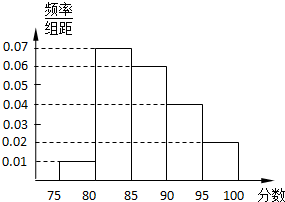 某高校在2013年考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示,
某高校在2013年考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示,