题目内容
定义在R上的函数f(x)=
ax3+bx2+cx+2同时满足以下条件:
①f(x)在(0,1)上是减函数,在(1,+∞)上是增函数;
②f′(x)是偶函数;
③f(x)在x=0处的切线与直线y=x+2垂直.
(Ⅰ)求函数y=f(x)的解析式;
(Ⅱ)设g(x)=[
x3-f(x)]•ex,求函数g(x)在[m,m+1]上的最小值.
| 1 |
| 3 |
①f(x)在(0,1)上是减函数,在(1,+∞)上是增函数;
②f′(x)是偶函数;
③f(x)在x=0处的切线与直线y=x+2垂直.
(Ⅰ)求函数y=f(x)的解析式;
(Ⅱ)设g(x)=[
| 1 |
| 3 |
(Ⅰ)求导函数,可得f′(x)=ax2+2bx+c…(1分)
由题意知
,即
解得
.…(4分)
所以函数y=f(x)的解析式为f(x)=
x3-x+2.…(5分)
(Ⅱ)g(x)=(
x3-f(x))ex=(x-2)ex,∴g′(x)=(x-1)ex.
令g′(x)=0得x=1,所以函数g(x)在(-∞,1)递减,在(1,+∞)递增..…(7分)
当m≥1时,g(x)在[m,m+1]单调递增,ymin=g(m)=(m-2)em…(9分)
当m<1<m+1,即0<m<1时,g(x)在[m,1]单调递减,在[1,m+1]单调递增,ymin=g(1)=-e..…(10分)
当m+1≤1,即m≤0时,g(x)在[m,m+1]单调递减,ymin=g(m+1)=(m-1)em+1.….(12分)
综上,g(x)在[m,m+1]上的最小值ymin=
.…(13分)
由题意知
|
|
|
所以函数y=f(x)的解析式为f(x)=
| 1 |
| 3 |
(Ⅱ)g(x)=(
| 1 |
| 3 |
令g′(x)=0得x=1,所以函数g(x)在(-∞,1)递减,在(1,+∞)递增..…(7分)
当m≥1时,g(x)在[m,m+1]单调递增,ymin=g(m)=(m-2)em…(9分)
当m<1<m+1,即0<m<1时,g(x)在[m,1]单调递减,在[1,m+1]单调递增,ymin=g(1)=-e..…(10分)
当m+1≤1,即m≤0时,g(x)在[m,m+1]单调递减,ymin=g(m+1)=(m-1)em+1.….(12分)
综上,g(x)在[m,m+1]上的最小值ymin=
|

练习册系列答案
相关题目
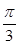 ,x=
,x=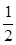
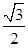
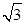

 =_______.
=_______. 等于( )
等于( )


