题目内容
（本题满分14分）在数列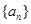
中，
，
，
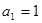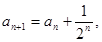（1）求数列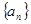
的通项公式；
（2）求数列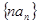
的前
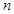项和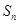
；
（3）在（2）的条件下指出数列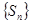
的最小项的值，并证明你的结论。
【答案】
（1）
(
)；
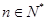（2）
=
；
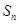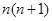
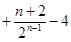（3）
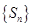的最小项为
【解析】本试题主要是考查了数列中通项公式的求解，以及数列的求和的综合运用。
（1）因为由已知有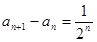
利用累差迭加即可求出数列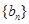
的通项公式
（2）结合第一问可知由（I）知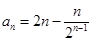
,
=
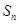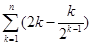
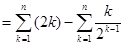，利用错位相减法得到。
(3)利用定义法得到数列的单调性，进而求解数列的最小项的求解的综合运用。
解：（1）由已知有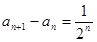
利用累差迭加即可求出数列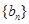的通项公式:
()
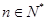------------------------ - 4分
2）由（I）知,=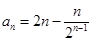
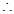
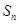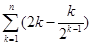
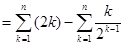
而
,
对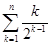
用错位相减法，易得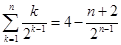
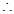
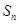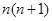
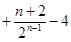=----------------10分
（3）
-
=
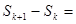
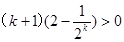
----------------14分
练习册系列答案
相关题目
（
），
，动点
的轨迹为T．
时，已知
、
，试探究是否存在这样的点
： 
？若存在，求出点Q的坐标，若不存在，说明理由．
中，已知圆
，
．
的直线
被圆
截得的弦长为
，求直线
是以1为半径，圆心在圆
：
上移动的动圆 ，若圆
分别作圆
的两条切线
，切点为
，求
的取值范围 ；
同时平分圆
的周长、圆
中，角
、
、
所对应的边分别为
、
、
，且满足
，求实数
的值。
，求
的值.
的正方体
中,
是线段
的中点,底面ABCD的中心是F.
^
； 
；
的体积。
的左、右焦点分别为F1、F2．F2也是抛物线C2：
的焦点，点M为C1与C2在第一象限的交点，且
．
，直线l∥MN，且与C1交于A、B两点，若
·
=0，求直线l的方程．