题目内容
已知抛物线y2=4x的焦点为F,过点F的直线交抛物线于A,B两点,且点A在第一象限.
(Ⅰ)若
=2
,求直线AB的斜率;
(Ⅱ)求三角形OAB面积的最小值(O为坐标原点).
(Ⅰ)若
| AF |
| FB |
(Ⅱ)求三角形OAB面积的最小值(O为坐标原点).
分析:(Ⅰ)把直线的方程与抛物线的方程联立,利用根与系数的关系、向量共线即可得出;
(Ⅱ)利用(Ⅰ)的结论、三角形的面积公式即可得出.
(Ⅱ)利用(Ⅰ)的结论、三角形的面积公式即可得出.
解答:解:(Ⅰ)∵抛物线y2=4x,∴焦点F(1,0).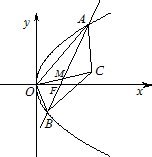
设直线AB方程为x=my+1,A(x1,y1),B(x2,y2),
将直线AB的方程与抛物线的方程联立
,消去x得y2-4my-4=0.
∴y1+y2=4m,y1y2=-4. ①
∵
=2
,
∴y1=-2y2. ②
联立①和②,消去y1,y2,得m=
.
∴直线AB的斜率是2
.
(Ⅱ)由(Ⅰ)可知:|y1-y2|=
=
=4
.
∵S△AOB=
|OF| |y1-y2|
∴S△AOB=2
,
∴m=0时,△OAB的面积最小,最小值是2.

设直线AB方程为x=my+1,A(x1,y1),B(x2,y2),
将直线AB的方程与抛物线的方程联立
|
∴y1+y2=4m,y1y2=-4. ①
∵
| AF |
| FB |
∴y1=-2y2. ②
联立①和②,消去y1,y2,得m=
| ||
| 4 |
∴直线AB的斜率是2
| 2 |
(Ⅱ)由(Ⅰ)可知:|y1-y2|=
| (y1+y2)2-4y1y2 |
| 16m2+16 |
| 1+m2 |
∵S△AOB=
| 1 |
| 2 |
∴S△AOB=2
| 1+m2 |
∴m=0时,△OAB的面积最小,最小值是2.
点评:本题考查了直线与抛物线的相交问题,熟练掌握一元二次方程的根与系数的关系、向量共线、直线的斜率、三角形的面积公式是解题的关键.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
 已知抛物线y2=4x,焦点为F,顶点为O,点P(m,n)在抛物线上移动,Q是OP的中点,M是FQ的中点.
已知抛物线y2=4x,焦点为F,顶点为O,点P(m,n)在抛物线上移动,Q是OP的中点,M是FQ的中点.