题目内容
(1)已知函数f(x)=rx-xr+(1-r)(x>0),其中r为有理数,且0<r<1,求f(x)的最小值;
(2)试用(1)的结果证明如下命题:设a1≥0,a2≥0,b1,b2为正有理数,若b1+b2=1,则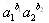 ≤a1b1+a2b2;
≤a1b1+a2b2;
(3)请将(2)中的命题推广到一般形式,并用数学归纳法证明你所推广的命题。注:当α为正有理数时,有求导公式(xα)′=αxα-1 。
(2)试用(1)的结果证明如下命题:设a1≥0,a2≥0,b1,b2为正有理数,若b1+b2=1,则
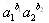 ≤a1b1+a2b2;
≤a1b1+a2b2;(3)请将(2)中的命题推广到一般形式,并用数学归纳法证明你所推广的命题。注:当α为正有理数时,有求导公式(xα)′=αxα-1 。
解:(1)求导函数可得:f′(x)=r(1-xr-1),
令f′(x)=0,解得x=1;
当0<x<1时,f′(x)<0,
所以f(x)在(0,1)上是减函数;
当x>1时,f′(x)>0,
所以f(x)在(0,1)上是增函数
所以f(x)在x=1处取得最小值f(1)=0;
(2)由(1)知,x∈(0,+∞)时,有f(x)≥f(1)=0,即xr≤rx+(1-r)①
若a1,a2中有一个为0,
则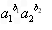 ≤a1b1+a2b2成立;
≤a1b1+a2b2成立;
若a1,a2均不为0,
∵b1+b2=1,
∴b2=1-b1,
∴①中令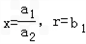 ,可得
,可得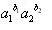 ≤a1b1+a2b2成立
≤a1b1+a2b2成立
综上,对a1≥0,a2≥0,b1,b2为正有理数,
若b1+b2=1,则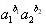 ≤a1b1+a2b2;② 。
≤a1b1+a2b2;② 。
(3)(2)中的命题推广到一般形式为:设a1≥0,a2≥0,…,an≥0,b1,b2,…,bn为正有理数,若b1+b2+…+bn=1,则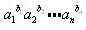 ≤a1b1+a2b2+…anbn;③
≤a1b1+a2b2+…anbn;③
用数学归纳法证明:
(i)当n=1时,b1=1,a1≤a1,③成立
(ii)假设当n=k时,③成立,即a1≥0,a2≥0,…,ak≥0,b1,b2,…,bk为正有理数,若
b1+b2+…+bk=1,则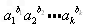 ≤a1b1+a2b2+…akbk
≤a1b1+a2b2+…akbk
当n=k+1时,a1≥0,a2≥0,…,ak+1≥0,b1,b2,…,bk+1为正有理数,
若b1+b2+…+bk+1=1,
则1-bk+1>0
于是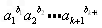 =(
=(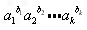 )
)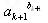 =
= 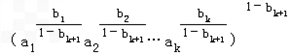
∵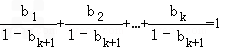
∴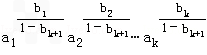 ≤
≤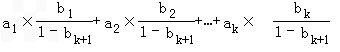
=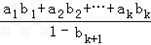
∴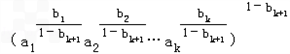
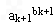 ≤
≤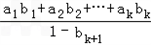 ·(1-bk+1)
·(1-bk+1)
∴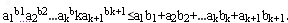
∴当n=k+1时,③
成立由(i)(ii)可知,对一切正整数,推广的命题成立。
令f′(x)=0,解得x=1;
当0<x<1时,f′(x)<0,
所以f(x)在(0,1)上是减函数;
当x>1时,f′(x)>0,
所以f(x)在(0,1)上是增函数
所以f(x)在x=1处取得最小值f(1)=0;
(2)由(1)知,x∈(0,+∞)时,有f(x)≥f(1)=0,即xr≤rx+(1-r)①
若a1,a2中有一个为0,
则
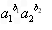 ≤a1b1+a2b2成立;
≤a1b1+a2b2成立;若a1,a2均不为0,
∵b1+b2=1,
∴b2=1-b1,
∴①中令
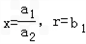 ,可得
,可得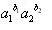 ≤a1b1+a2b2成立
≤a1b1+a2b2成立综上,对a1≥0,a2≥0,b1,b2为正有理数,
若b1+b2=1,则
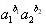 ≤a1b1+a2b2;② 。
≤a1b1+a2b2;② 。(3)(2)中的命题推广到一般形式为:设a1≥0,a2≥0,…,an≥0,b1,b2,…,bn为正有理数,若b1+b2+…+bn=1,则
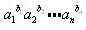 ≤a1b1+a2b2+…anbn;③
≤a1b1+a2b2+…anbn;③ 用数学归纳法证明:
(i)当n=1时,b1=1,a1≤a1,③成立
(ii)假设当n=k时,③成立,即a1≥0,a2≥0,…,ak≥0,b1,b2,…,bk为正有理数,若
b1+b2+…+bk=1,则
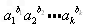 ≤a1b1+a2b2+…akbk
≤a1b1+a2b2+…akbk当n=k+1时,a1≥0,a2≥0,…,ak+1≥0,b1,b2,…,bk+1为正有理数,
若b1+b2+…+bk+1=1,
则1-bk+1>0
于是
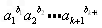 =(
=(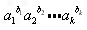 )
)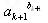 =
= 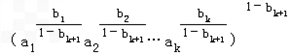
∵
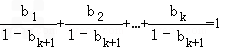
∴
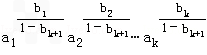 ≤
≤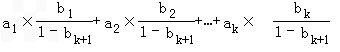
=
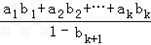
∴
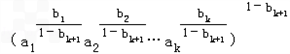
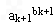 ≤
≤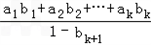 ·(1-bk+1)
·(1-bk+1)∴
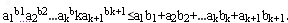
∴当n=k+1时,③
成立由(i)(ii)可知,对一切正整数,推广的命题成立。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目