题目内容
对于非空实数集 ,定义
,定义 .设非空实数集
.设非空实数集 .现给出以下命题:
.现给出以下命题:
(1)对于任意给定符合题设条件的集合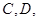 必有
必有
(2)对于任意给定符合题设条件的集合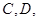 必有
必有 ;
;
(3)对于任意给定符合题设条件的集合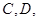 必有
必有 ;
;
(4)对于任意给定符合题设条件的集合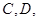 必存在常数
必存在常数 ,使得对任意的
,使得对任意的 ,恒有
,恒有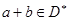 .
.
以上命题正确的是
(1)(4)
解析试题分析:(1)对任意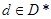 ,根据题意,对任意
,根据题意,对任意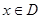 ,有
,有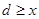 ,因为
,因为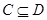 ,所以对任意的
,所以对任意的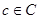 ,一定有
,一定有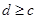 ,所以
,所以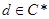 ,即
,即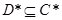 ,(1)正确;(2)如
,(1)正确;(2)如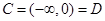 ,则
,则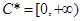 ,但
,但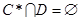 ,(2)错误;(3)如如
,(2)错误;(3)如如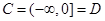 ,则
,则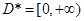 ,但
,但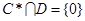 ,(3)错误;(4)首先对任意集合
,(3)错误;(4)首先对任意集合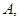 由定义知
由定义知 一定有最小值,又由(1)
一定有最小值,又由(1)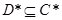 ,设
,设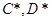 的最小值分别为
的最小值分别为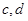 ,即
,即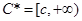 ,
,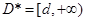 ,只要取
,只要取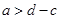 ,则对任意的
,则对任意的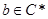 ,
, ,即
,即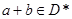 ,(4)正确,故(1)(4)正确.
,(4)正确,故(1)(4)正确.
考点:新定义概念,集合的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
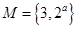 ,
,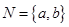 .若
.若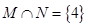 ,则
,则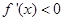 .
.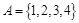 ,
,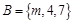 ,若
,若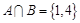 ,则
,则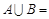 .
.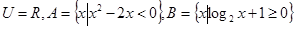 ,则
,则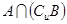 =
=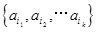 ,定义X的“特征数列”为x1,x2…,x100,其中
,定义X的“特征数列”为x1,x2…,x100,其中 =
=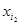 =…=
=…=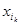 =1.其余项均为0,例如:子集{a2,a3}的“特征数列”为0,1,1,0,0,…,0.
=1.其余项均为0,例如:子集{a2,a3}的“特征数列”为0,1,1,0,0,…,0.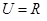 ,函数
,函数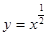 的值域为集合
的值域为集合 ,则
,则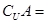 .
. A∩B}.若A={x|y=
A∩B}.若A={x|y= },B={y|y=3x},则A×B=________.
},B={y|y=3x},则A×B=________.