题目内容
(本小题12分) 已知曲线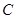
 的极坐标方程为
的极坐标方程为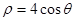 ,曲线
,曲线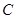
 的方程是
的方程是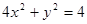 , 直线
, 直线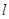 的参数方程是:
的参数方程是: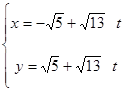
 .
.
(1)求曲线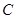
 的直角坐标方程,直线
的直角坐标方程,直线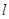 的普通方程;
的普通方程;
(2)求曲线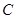
 上的点到直线
上的点到直线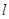 距离的最小值.
距离的最小值.
解: (1)  ;(2)到直线
;(2)到直线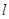 距离的最小值为
距离的最小值为 。
。
解析试题分析:(Ⅰ)利用直角坐标与极坐标间的关系:ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得C的直角坐标方程,将直线l的参数消去得出直线l的普通方程.
(Ⅱ)曲线C1的方程为4x2+y2=4,设曲线C1上的任意点(cosθ,2sinθ),利用点到直线距离公式,建立关于θ的三角函数式求解.
解: (1) 曲线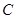
 的方程为
的方程为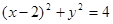 ,直线
,直线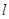 的方程是:
的方程是:
(2)设曲线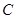
 上的任意点
上的任意点 ,
,
该点到直线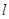 距离
距离 .
.
到直线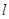 距离的最小值为
距离的最小值为 。
。
考点:本题主要考查了曲线参数方程求解、应用.考查函数思想,三角函数的性质.属于中档题.
点评:解决该试题的关键是对于椭圆上点到直线距离的最值问题,一般用参数方程来求解得到。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知某企业上半年前5个月产品广告投入与利润额统计如下:
| 月份 | 1 | 2 | 3 | 4 | 5 |
| 广告投入(x万元) | 9.5 | 9.3 | 9.1 | 8.9 | 9.7 |
| 利润(y万元) | 92 | 89 | 89 | 87 | 93 |
由此所得回归方程为
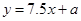 ,若6月份广告投入10(万元)估计所获利润为( )
,若6月份广告投入10(万元)估计所获利润为( )A.95.25万元 B.96.5万元 C.97万元 D.97.25万元
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,一般情况下PM2.5的浓度越大,大气环境质量越差.右边的茎叶图表示的是成都市区甲乙两个监测站某10日内每天的PM2.5浓度读数(单位: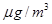 ),则下列说法正确的是( )
),则下列说法正确的是( )
| A.这10日内甲、乙监测站读数的极差相等 |
| B.这10日内甲、乙监测站读数的中位数中,乙的较大 |
| C.这10日内乙监测站读数的众数与中位数相等 |
| D.这10日内甲、乙监测站读数的平均数相等 |

 中,曲线
中,曲线 的参数方程为
的参数方程为 为参数),以该直角坐标系的原点
为参数),以该直角坐标系的原点 为极点,
为极点, 轴的正半轴为极轴的极坐标系下,曲线
轴的正半轴为极轴的极坐标系下,曲线 的方程为
的方程为 .
. 、
、 ,求
,求 .
.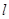 是过点
是过点 ,方向向量为
,方向向量为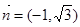 的直线。圆方程
的直线。圆方程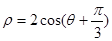
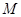 、
、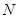 两点,求
两点,求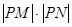 的值。
的值。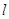 经过点
经过点 ,倾斜角
,倾斜角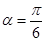 ,
,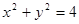 相交于
相交于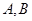 两点,求点
两点,求点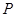 到
到 坐标是
坐标是 ,曲线
,曲线 的方程为
的方程为 ;以极点为坐标原点,极轴为
;以极点为坐标原点,极轴为 轴的正半轴建立平面直角坐标系,斜率是
轴的正半轴建立平面直角坐标系,斜率是 的直线
的直线 经过点
经过点 、
、 ,并求
,并求 的值.
的值.
 (
( 为参数)和直线
为参数)和直线 (其中为参数,
(其中为参数, 为直线的倾斜角),如果直线与圆
为直线的倾斜角),如果直线与圆 有公共点,求
有公共点,求 的方程为x-y+4=0,曲线C的参数方程为
的方程为x-y+4=0,曲线C的参数方程为
 ,判断点P与直线
,判断点P与直线