题目内容
在数列{an}中,Sn为其前n项和,满足Sn=kan+n2-n(k∈R,n∈N*),
(Ⅰ)若k=1,求数列{an}的通项公式;
(Ⅱ)若数列{an-2n-1}为公比不为1的等比数列,求Sn。
(Ⅰ)若k=1,求数列{an}的通项公式;
(Ⅱ)若数列{an-2n-1}为公比不为1的等比数列,求Sn。
解:(1)当k=1时,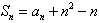 ,
,
所以 ,
,
所以当n=1时, ;
;
当n≥2时,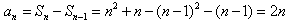 ,
,
所以数列{an}的通项公式为 。
。
(Ⅱ)当n≥2时, ,
,
 ,
,
若k=1,则 ,
,
从而 为公比为1的等比数列,不合题意;
为公比为1的等比数列,不合题意;
若k≠1,则 ,
,
 ,
,
由题意得, ,
,
当k=0时, ,不合题意;
,不合题意;
当 ,
,
从而 ,
,
因为 ,
,
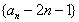 为公比为3的等比数列,
为公比为3的等比数列,
 ,
,
从而 。
。
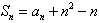 ,
,所以
 ,
,所以当n=1时,
 ;
;当n≥2时,
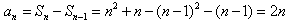 ,
,所以数列{an}的通项公式为
 。
。(Ⅱ)当n≥2时,
 ,
, ,
,若k=1,则
 ,
,从而
 为公比为1的等比数列,不合题意;
为公比为1的等比数列,不合题意;若k≠1,则
 ,
, ,
,由题意得,
 ,
,当k=0时,
 ,不合题意;
,不合题意;当
 ,
,从而
 ,
,因为
 ,
,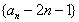 为公比为3的等比数列,
为公比为3的等比数列, ,
,从而
 。
。
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
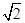 ,S3=12+
,S3=12+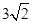 .
.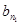 ,
,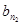 ,…,
,…,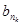 ,…成等比数列,其中n1=1,n2=3,求nk(用k表示);
,…成等比数列,其中n1=1,n2=3,求nk(用k表示);