题目内容
已知等差数列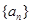 的首项
的首项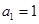 ,公差
,公差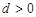 .且
.且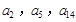 分别是等比数列
分别是等比数列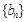 的
的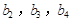 .
.
(Ⅰ)求数列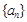 与
与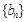 的通项公式;
的通项公式;
(Ⅱ)设数列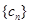 对任意自然数
对任意自然数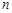 均有
均有
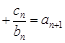 成立,求
成立,求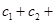
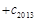 的值.
的值.
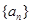 的首项
的首项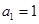 ,公差
,公差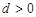 .且
.且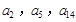 分别是等比数列
分别是等比数列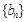 的
的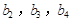 .
. (Ⅰ)求数列
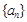 与
与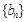 的通项公式;
的通项公式;(Ⅱ)设数列
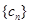 对任意自然数
对任意自然数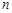 均有
均有
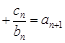 成立,求
成立,求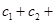
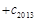 的值.
的值.(Ⅰ)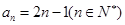 ,
, 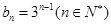 ;(Ⅱ)
;(Ⅱ)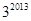 .
.
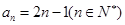 ,
, 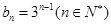 ;(Ⅱ)
;(Ⅱ)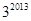 .
.试题分析:(Ⅰ)根据等比中项的定义列出等式,求出等差数列
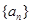 的公差,从而求出数列
的公差,从而求出数列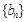 的公比
的公比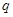 ,便可得到通向公式;(Ⅱ)按已知等式的规律写出
,便可得到通向公式;(Ⅱ)按已知等式的规律写出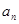 ,再两式相减,得出数列
,再两式相减,得出数列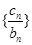 即是等差数列,变形求得数列
即是等差数列,变形求得数列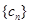 的通向公式,用公式求和.
的通向公式,用公式求和.试题解析:(Ⅰ)∵
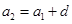 ,
,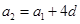 ,
,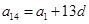 ,且
,且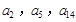 成等比数列
成等比数列∴
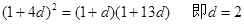 2分
2分∴
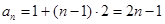 4分
4分又∵
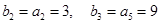 .
. ∴
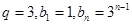 6分
6分(Ⅱ)∵

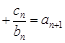 ①
①∴
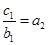 即
即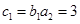
又

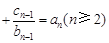 ②
②①-②:
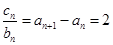 8分
8分∴
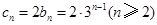
∴
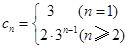 10分
10分则
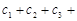
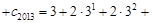
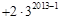

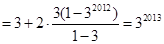 12分
12分
练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
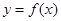 的图象经过坐标原点,其导函数为
的图象经过坐标原点,其导函数为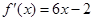 ,数列
,数列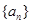 的前
的前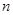 项和为
项和为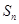 ,点
,点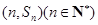 均在函数
均在函数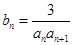 ,
,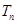 是数列
是数列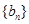 的前n项和,求使得
的前n项和,求使得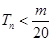 对所有
对所有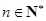 都成立的最小正整数
都成立的最小正整数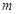 .
.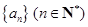 的前
的前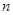 项和为
项和为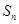 ,且
,且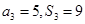 .
.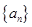 的通项公式;
的通项公式;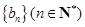 ,若
,若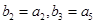 ,求数列
,求数列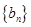 的前
的前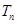 .
.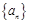 是首项为1,公差为
是首项为1,公差为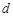 的等差数列,数列
的等差数列,数列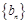 是首项为1,公比为
是首项为1,公比为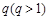 的等比
的等比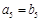 ,
,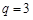 ,求数列
,求数列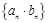 的前
的前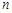 项和;
项和;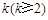 ,使得
,使得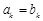 .试比较
.试比较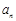 与
与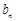 的大小,并说明理由.
的大小,并说明理由.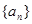 的前六项和为60,且
的前六项和为60,且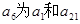 的等比中项.
的等比中项. 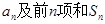 ;
;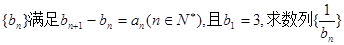 的前n项和
的前n项和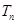 .
. 满足:存在正整数
满足:存在正整数 ,对于任意正整数
,对于任意正整数 都有
都有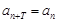 成立,则称数列
成立,则称数列 ,
,
 ,则
,则 可以取3个不同的值
可以取3个不同的值 ,则数列
,则数列 的数列
的数列 且
且 ,存在
,存在 ,
, 是周期为
是周期为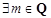 且
且 ,数列
,数列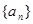 满足
满足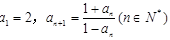 ,则该数列的前2013项的乘积______.
,则该数列的前2013项的乘积______. x
x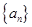 的公差
的公差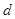 =1,前
=1,前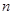 项和为
项和为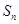 .
.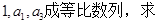
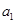 ;
;