题目内容
某创业投资公司拟投资开发某种新能源产品,估计能获得10万元~1000万元的投资收益.现准备制定一个对科研课题组的奖励方案:奖金y(单位:万元)随投资收益x(单位:万元)的增加而增加,且奖金不超过9万元,同时奖金不超过投资收益的20%.(Ⅰ)若建立函数模型制定奖励方案,试用数学语言表述公司对奖励函数模型的基本要求;
(Ⅱ)现有两个奖励函数模型:(1)y=
| x | 150 |
分析:(Ⅰ)设奖励函数模型为y=f(x),根据“奖金y(单位:万元)随投资收益x(单位:万元)的增加而增加,说明在定义域上是增函数,且奖金不超过9万元,即f(x)≤9,同时奖金不超过投资收益的20%.即f(x)≤
.
(Ⅱ)根据(I)去判断,(1)对于函数模型f(x)=
+2,由一次函数的性质研究,是否满足第一,二两个条件,构造函数
=
+
,由反比例函数性质研究是否满足第三个条件.
(2)对于函数模型f(x)=4lgx-3,由对数函数的性质研究
是否满足第一,二两个条件,再用作差法研究是否满足第三个条件即:4lgx-3-
<0,即4lgx-3<
,所以f(x)<
恒成立.
| x |
| 5 |
(Ⅱ)根据(I)去判断,(1)对于函数模型f(x)=
| x |
| 150 |
| f(x) |
| x |
| 1 |
| 150 |
| 2 |
| x |
(2)对于函数模型f(x)=4lgx-3,由对数函数的性质研究
是否满足第一,二两个条件,再用作差法研究是否满足第三个条件即:4lgx-3-
| x |
| 5 |
| x |
| 5 |
| x |
| 5 |
解答:解:(Ⅰ)设奖励函数模型为y=f(x),则公司对函数模型的基本要求是:
当x∈[10,1000]时,①f(x)是增函数;②f(x)≤9恒成立;③f(x)≤
恒成立.(3分)
(Ⅱ)(1)对于函数模型f(x)=
+2:
当x∈[10,1000]时,f(x)是增函数,则f(x)max=f(1000)=
+2=
+2<9.
所以f(x)≤9恒成立.(5分)
因为函数
=
+
在[10,1000]上是减函数,所以[
]max=
+
>
.
从而
=
+
≤
,即f(x)≤
不恒成立.
故该函数模型不符合公司要求.(8分)
(2)对于函数模型f(x)=4lgx-3:
当x∈[10,1000]时,f(x)是增函数,则f(x)max=f(1000)=4lg1000-3=9.
所以f(x)≤9恒成立.(10分)
设g(x)=4lgx-3-
,则g′(x)=
-
.
当x≥10时,g′(x)=
-
≤
=
<0,
所以g(x)在[10,1000]上是减函数,从而g(x)≤g(10)=-1<0.
所以4lgx-3-
<0,即4lgx-3<
,所以f(x)<
恒成立.
故该函数模型符合公司要求.(13分)
当x∈[10,1000]时,①f(x)是增函数;②f(x)≤9恒成立;③f(x)≤
| x |
| 5 |
(Ⅱ)(1)对于函数模型f(x)=
| x |
| 150 |
当x∈[10,1000]时,f(x)是增函数,则f(x)max=f(1000)=
| 1000 |
| 150 |
| 20 |
| 3 |
所以f(x)≤9恒成立.(5分)
因为函数
| f(x) |
| x |
| 1 |
| 150 |
| 2 |
| x |
| f(x) |
| x |
| 1 |
| 150 |
| 1 |
| 5 |
| 1 |
| 5 |
从而
| f(x) |
| x |
| 1 |
| 150 |
| 2 |
| x |
| 1 |
| 5 |
| x |
| 5 |
故该函数模型不符合公司要求.(8分)
(2)对于函数模型f(x)=4lgx-3:
当x∈[10,1000]时,f(x)是增函数,则f(x)max=f(1000)=4lg1000-3=9.
所以f(x)≤9恒成立.(10分)
设g(x)=4lgx-3-
| x |
| 5 |
| 4lge |
| x |
| 1 |
| 5 |
当x≥10时,g′(x)=
| 4lge |
| x |
| 1 |
| 5 |
| 2lge-1 |
| 5 |
| lge2-1 |
| 5 |
所以g(x)在[10,1000]上是减函数,从而g(x)≤g(10)=-1<0.
所以4lgx-3-
| x |
| 5 |
| x |
| 5 |
| x |
| 5 |
故该函数模型符合公司要求.(13分)
点评:本题主要考查函数模型的选择,其实质是考查函数的基本性质,同时,确定函数关系实质就是将文字语言转化为数学符号语言--数学化,再用数学方法定量计算得出所要求的结果,关键是理解题意,将变量的实际意义符号化.

练习册系列答案
相关题目
 ;(2)
;(2) .试问这两个函数模
.试问这两个函数模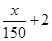 ;(2)y=4lgx-3.试分析这两个函数模型是否符合公司要求?
;(2)y=4lgx-3.试分析这两个函数模型是否符合公司要求?