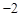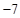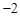题目内容
设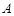 是由
是由 个实数组成的
个实数组成的 行
行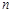 列的数表,如果某一行(或某一列)各数之和为负数,则改变该行(或该列)中所有数的符号,称为一次“操作”.
列的数表,如果某一行(或某一列)各数之和为负数,则改变该行(或该列)中所有数的符号,称为一次“操作”.
(Ⅰ) 数表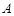 如表1所示,若经过两次“操作”,使得到的数表每行的各数之和与每列的各数之和均为非负实数,请写出每次“操作”后所得的数表(写出一种方法即可);
如表1所示,若经过两次“操作”,使得到的数表每行的各数之和与每列的各数之和均为非负实数,请写出每次“操作”后所得的数表(写出一种方法即可);
表1
|
1 |
2 |
3 |
|
|
|
1 |
0 |
1 |
(Ⅱ) 数表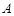 如表2所示,若必须经过两次“操作”,才可使得到的数表每行的各数之和与每列的各数之和均为非负整数,求整数
如表2所示,若必须经过两次“操作”,才可使得到的数表每行的各数之和与每列的各数之和均为非负整数,求整数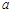 的所有可能值;
的所有可能值;
表2
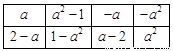
(Ⅲ)对由 个实数组成的
个实数组成的 行
行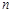 列的任意一个数表
列的任意一个数表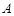 ,能否经过有限次“操作”以后,使得到的数表每行的各数之和与每列的各数之和均为非负整数?请说明理由.
,能否经过有限次“操作”以后,使得到的数表每行的各数之和与每列的各数之和均为非负整数?请说明理由.
(I) 详见解析; (II) 或
或 ;(Ⅲ) 能,理由详见解析.
;(Ⅲ) 能,理由详见解析.
【解析】
试题分析::(I)根据题中一次“操作”的含义,将原数表改变第4列,再改变第2行即可;或者改变第2行,改变第4列也可得(写出一种即可);(II) 每一列所有数之和分别为2,0,-2,0,每一行所有数之和分别为-1,1;①如果操作第三列,第一行之和为2a-1,第二行之和为5-2a,列出不等关系解得a,b范围进而分情况进行第二次操作;②如果操作第一行,易由条件得a的值;(III) 按要求对某行(或某列)操作一次时,则该行的行和(或该列的列和),由负数变为正数,都会引起该行的行和(或该列的列和)增大,从而也就使得数阵中mn个数之和增加.
解:法1:

法2:
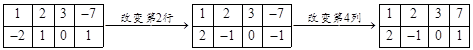
法3:

3分
(II) 每一列所有数之和分别为2,0,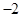 ,0,每一行所有数之和分别为
,0,每一行所有数之和分别为 ,1;
,1;
①如果首先操作第三列,则
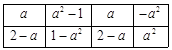
则第一行之和为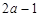 ,第二行之和为
,第二行之和为 ,
,
这两个数中,必须有一个为负数,另外一个为非负数,
所以  或
或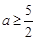
当 时,则接下来只能操作第一行,
时,则接下来只能操作第一行,

此时每列之和分别为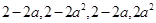
必有 ,解得
,解得
当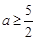 时,则接下来操作第二行
时,则接下来操作第二行

此时第4列和为负,不符合题意. 6分
② 如果首先操作第一行
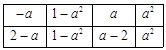
则每一列之和分别为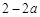 ,
, ,
, ,
,
当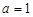 时,每列各数之和已经非负,不需要进行第二次操作,舍掉
时,每列各数之和已经非负,不需要进行第二次操作,舍掉
当 时,
时,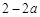 ,
, 至少有一个为负数,
至少有一个为负数,
所以此时必须有 ,即
,即 ,所以
,所以 或
或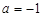
经检验, 或
或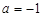 符合要求
符合要求
综上: 9分
9分
(III)能经过有限次操作以后,使得得到的数表所有的行和与所有的列和均为非负实数。证明如下:
记数表中第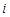 行第
行第 列的实数为
列的实数为 (
(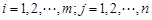 ),各行的数字之和分别为
),各行的数字之和分别为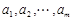 ,各列的数字之和分别为
,各列的数字之和分别为 ,
,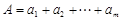 ,
,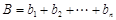 ,数表中
,数表中 个实数之和为
个实数之和为 ,则
,则 。记
。记
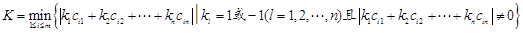

 .
.
按要求操作一次时,使该行的行和(或该列的列和)由负变正,都会引起 (和
(和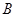 )增大,从而也就使得
)增大,从而也就使得 增加,增加的幅度大于等于
增加,增加的幅度大于等于 ,但是每次操作都只是改变数表中某行(或某列)各数的符号,而不改变其绝对值,显然,
,但是每次操作都只是改变数表中某行(或某列)各数的符号,而不改变其绝对值,显然, 必然小于等于最初的数表中
必然小于等于最初的数表中 个实数的绝对值之和,可见其增加的趋势必在有限次之后终止。终止之时,必是所有的行和与所有的列和均为非负实数,否则,只要再改变该行或该列的符号,
个实数的绝对值之和,可见其增加的趋势必在有限次之后终止。终止之时,必是所有的行和与所有的列和均为非负实数,否则,只要再改变该行或该列的符号, 就又会继续上升,导致矛盾,故结论成立。
13分
就又会继续上升,导致矛盾,故结论成立。
13分
考点:推理与证明.

设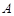 是由
是由 个实数组成的
个实数组成的 行
行 列的数表,如果某一行(或某一列)各数之和为负数,则改变该行(或该列)中所有数的符号,称为一次“操作”.
列的数表,如果某一行(或某一列)各数之和为负数,则改变该行(或该列)中所有数的符号,称为一次“操作”.
(1)数表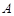 如表1所示,若经过两“操”,使得到的数表每行的各数之和与每列的各数之和均为非负实数,请写出每次“操作”后所得的数表(写出一种方法即可);表1
如表1所示,若经过两“操”,使得到的数表每行的各数之和与每列的各数之和均为非负实数,请写出每次“操作”后所得的数表(写出一种方法即可);表1
|
1 |
2 |
3 |
|
|
|
1 |
0 |
1 |

(2)数表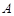 如表2所示,若必须经过两次“操作”,才可使得到的数表每行的各数之和与每列的各数之和均为非负整数,求整数
如表2所示,若必须经过两次“操作”,才可使得到的数表每行的各数之和与每列的各数之和均为非负整数,求整数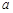 的所有可能值;表2
的所有可能值;表2
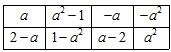
(3)对由 个实数组成的
个实数组成的 行
行 列的任意一个数表
列的任意一个数表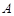 ,能否经过有限次“操作”以后,使得到的数表每行的各数之和与每列的各数之和均为非负实数?请说明理由.
,能否经过有限次“操作”以后,使得到的数表每行的各数之和与每列的各数之和均为非负实数?请说明理由.
设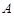 是由
是由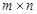 个实数组成的
个实数组成的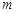 行
行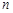 列的数表,如果某一行(或某一列)各数之和为负数,则改变该行(或该列)中所有数的符号,称为一次“操作”.
列的数表,如果某一行(或某一列)各数之和为负数,则改变该行(或该列)中所有数的符号,称为一次“操作”.
(Ⅰ) 数表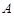 如表所示,若经过两次“操作”,使得到的数表每行的各数之和与每列的各数之和均为非负实数,请写出每次“操作”后所得的数表(写出一种方法即可);
如表所示,若经过两次“操作”,使得到的数表每行的各数之和与每列的各数之和均为非负实数,请写出每次“操作”后所得的数表(写出一种方法即可);
|
1 |
2 |
3 |
|
|
|
1 |
0 |
1 |
(Ⅱ) 数表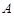 如表所示,若必须经过两次“操作”,才可使得到的数表每行的各数之和与每列的各数之和均为非负整数,求整数
如表所示,若必须经过两次“操作”,才可使得到的数表每行的各数之和与每列的各数之和均为非负整数,求整数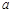 的所有可能值;
的所有可能值;
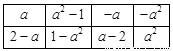
(Ⅲ)对由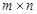 个实数组成的
个实数组成的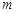 行
行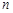 列的任意一个数表
列的任意一个数表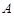 ,
,
能否经过有限次“操作”以后,使得到的数表每行的各数之
和与每列的各数之和均为非负整数?请说明理由.
(2012年高考(北京理))设A是由![]() 个实数组成的
个实数组成的![]() 行
行![]() 列的数表,满足:每个数的绝对值不大于1,且所有数的和为零.记
列的数表,满足:每个数的绝对值不大于1,且所有数的和为零.记![]() 为所有这样的数表构成的集合.
为所有这样的数表构成的集合.
对于![]() ,记
,记![]() 为A的第
为A的第![]() 行各数之和
行各数之和![]() ,
,![]() 为A的第
为A的第![]() 列各数之和
列各数之和![]() ;
;
记![]() 为
为![]() ,
,![]() ,…,
,…,![]() ,
,![]() ,
,![]() ,…,
,…,![]() 中的最小值.
中的最小值.
(1)对如下数表A,求![]() 的值;
的值;
| 1 | 1 | -0.8 |
| 0.1 | -0.3 | -1 |
(2)设数表A=![]() 形如
形如
| 1 | 1 | 1 |
|
|
| -1 |
求![]() 的最大值;
的最大值;
(3)给定正整数![]() ,对于所有的A∈S(2,
,对于所有的A∈S(2,![]() ),求
),求![]() 的最大值。
的最大值。