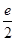题目内容
若a>0,b>0,且函数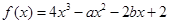 在x=1处有极值,则ab的最大值等于( )
在x=1处有极值,则ab的最大值等于( )
| A.2 | B.9 | C.6 | D.3 |
B
解析试题分析:求出导函数,利用函数在极值点处的导数值为0得到a,b满足的条件;利用基本不等式求出ab的最值,即∵f′(x)=12x2-2ax-2b,又因为在x=1处有极值,f’(1)=0,故有a+b=6,∵a>0,b>0,∴ab≤(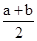 )2=9,当且仅当a=b=3时取等号,所以ab的最大值等于9,选B
)2=9,当且仅当a=b=3时取等号,所以ab的最大值等于9,选B
考点:本试题主要考查了函数在极值点处的导数值为0、考查利用基本不等式求最值需注意:一正、二定、三相等.
点评:注意利用基本不等式求最值需注意:一正、二定、三相等条件缺一不可。

练习册系列答案
相关题目
已知函数 在
在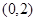 上恰有两个零点,则实数
上恰有两个零点,则实数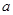 的取值范围为( )
的取值范围为( )
A.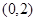 | B.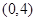 | C. | D.(2,4) |
曲线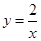 与直线
与直线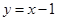 及
及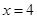 所围成的封闭图形的面积为
所围成的封闭图形的面积为
A.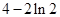 | B.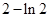 | C.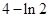 | D.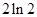 |
直线y=x与抛物线 y=x(x+2)所围成的封闭图形的面积等于
y=x(x+2)所围成的封闭图形的面积等于
A.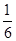 | B.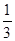 | C.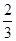 | D.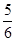 |
由曲线 ,
,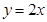 围成的封闭图形的面积为( )
围成的封闭图形的面积为( )
A.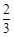 | B.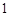 | C.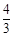 | D.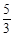 |
 是函数
是函数 的导函数,
的导函数,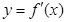 的图象如图所示,则
的图象如图所示,则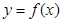 的图象最有可能的是( )
的图象最有可能的是( )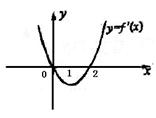
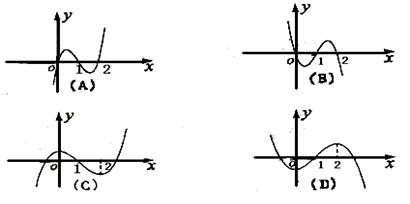
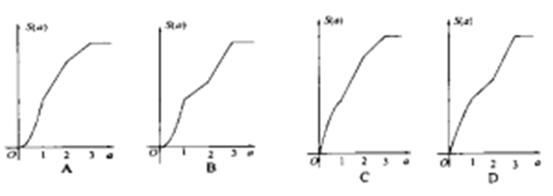
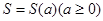 是图1中阴影部分介于平等线
是图1中阴影部分介于平等线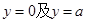 之间的那一部分的面积,则函数
之间的那一部分的面积,则函数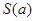 的图象大致为( )
的图象大致为( )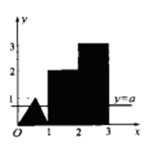
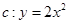 ,点
,点 及点
及点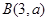 ,从点A观察B,要实现不被曲线C挡住,则实数
,从点A观察B,要实现不被曲线C挡住,则实数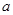 的取值范围是( )
的取值范围是( )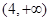
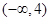
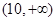
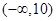
 :
: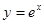 在点
在点 处的切线
处的切线 恰好经过坐标原点,则曲线
恰好经过坐标原点,则曲线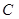 、直线
、直线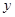 轴围成的图形面积为 ( )
轴围成的图形面积为 ( )