Question

（本小题满分12分）已知函数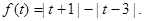
（I）求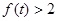的解集；
（II）设a>0,g(x)=ax²－2x＋5, 若对任意实数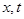，均有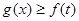恒成立，求a的取值范围。

Answer 1

（1）t＞2 (2)a≥1

解析试题分析：解：（1）因为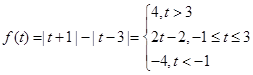,故可知，当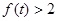时，则可知t＞2
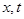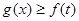(2)因为要使得a>0,g(x)=ax²－2x＋5, 若对任意实数，均有恒成立
即ax²－2x＋5，即可知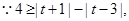 ax²－2x＋5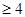恒成立，根据二次函数的性质可知，开口向上，判别式小于等于零，可知a≥1
考点：分段函数，一元二次不等式等知识。
点评：以函数为背景考查了一元二次不等式的求解，以及不等式恒成立问题，考查了等价转化思想，属于中档题。