题目内容
已知函数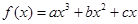 在点
在点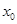 处取得极小值-4,使其导数
处取得极小值-4,使其导数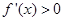 的
的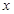 的取值范围为
的取值范围为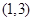 ,求:
,求:
(1)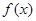 的解析式;
的解析式;
(2)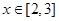 ,求
,求 的最大值;
的最大值;
【答案】
(1) (2)当
(2)当 时
时 ,当
,当 时
时 ,当
,当 时
时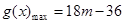
【解析】
试题分析:⑴
 ,导数
,导数 的
的 的取值范围为
的取值范围为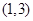 ,所以
,所以 ,点
,点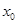 处取得极小值-4
处取得极小值-4  ,联立方程求解得
,联立方程求解得 ,所以
,所以
⑵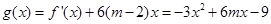 ,对称轴为
,对称轴为
当 时,最大值为
时,最大值为 ,
,
当 时,最大值为
时,最大值为 ,
,
当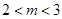 时,最大值为
时,最大值为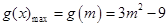
考点:函数导数及单调性最值
点评:利用函数在极值点处导数为0来确定极值点的位置,第二问中函数含有参数,求最值需按对称轴的位置分情况讨论函数取得的最值

练习册系列答案
相关题目
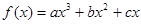 在点
在点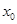 处取得极小值-4,使其导数
处取得极小值-4,使其导数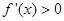 的
的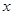 的取值范围为
的取值范围为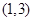 ,求:
,求: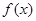 的解析式;
的解析式;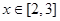 ,求
,求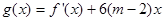 的最大值;
的最大值;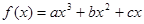 在点
在点 处取得极小值-4,使其导函数
处取得极小值-4,使其导函数 的
的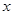 的取值范围为(1,3)
的取值范围为(1,3) 的解析式及
的解析式及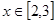 时,求
时,求 的最大值。
的最大值。