题目内容
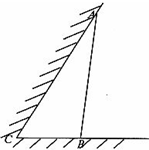如图所示，某饲养场要建造一间两面靠墙的三角形露天养殖场，已知已有两面墙的夹角为60°（即∠C=60°），现有可供建造第三面围墙的材料60米（两面墙的长均大于60米），为了使得小老虎能健康成长，要求所建造的三角形露天活动室尽可能大，记∠ABC=θ．（1）问当θ为多少时，所建造的三角形露天活动室的面积最大？
（2）若饲养场建造成扇形，养殖场的面积能比（1）中的最大面积更大？说明理由．
分析：（1）利用余弦定理列出关系式，将c，cosC的值代入并利用基本不等式求出ab的最大值，利用三角形的面积公式求出面积的最大值，以及此时θ的值；
（2）利用弧长公式求出AC，再利用扇形面积公式表示出扇形面积，与第一问面积的最大值比较即可得到结果．
（2）利用弧长公式求出AC，再利用扇形面积公式表示出扇形面积，与第一问面积的最大值比较即可得到结果．
解答：解：（1）在△ABC中，由余弦定理：c2=602=a2+b2-2abcos60°，
∴a2+b2-ab=3600，
∴3600+ab=a2+b2≥2ab，即ab≤3600，
∴S△ABC=
AC•BC•sin
=
ab≤900
，
此时a=b，△ABC为等边三角形，
∴θ=60°，（S△ABC）max=900
；
（2）若饲养场建造成扇形时，由60=
×AC，得AC=
，
∴S扇形=
×60×
=
，
∵900
=
≤
，
∴养殖场建造成扇形时面积能比（1）中的最大面积更大．
∴a2+b2-ab=3600，
∴3600+ab=a2+b2≥2ab，即ab≤3600，
∴S△ABC=
| 1 |
| 2 |
| π |
| 3 |
| ||
| 4 |
| 3 |
此时a=b，△ABC为等边三角形，
∴θ=60°，（S△ABC）max=900
| 3 |
（2）若饲养场建造成扇形时，由60=
| π |
| 3 |
| 180 |
| π |
∴S扇形=
| 1 |
| 2 |
| 180 |
| π |
| 5400 |
| π |
∵900
| 3 |
| 5400 | ||
2
|
| 5400 |
| π |
∴养殖场建造成扇形时面积能比（1）中的最大面积更大．
点评：此题考查了余弦定理，基本不等式的应用，熟练掌握余弦定理是解本题的关键．
练习册系列答案
相关题目
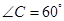），现有可供建造第三面围墙的材料60米（两面墙的长均大于60米），为了使得小老虎能健康成长，要求所建造的三角形露天活动室尽可能大，记
，
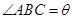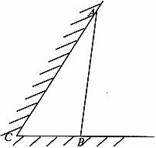
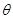为多少时，所建造的三角形露天活动室的面积最大？