Question

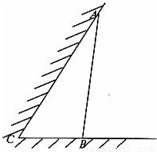
如图所示，某动物园要为刚入园的小老虎建造一间两面靠墙的三角形露天活动室，已知已有的两面墙的夹角为60°（即∠C=60°且两面墙的长度足够大），现有可供建造第三面围墙的材料6米（即AB长为6米），为了使得小老虎能健康成长，要求所建造的三角形露天活动室尽可能大，记∠ABC=θ．
（1）当θ=105°时，求所建造的三角形露天活动室的面积．
（2）问当θ为多少时，所建造的三角形露天活动室的面积最大？

Answer 1

分析：由正弦定理易得，AC=4

3

•sinθ，BC=4

3

•sin(θ+

π

3

)
（1）当θ=105°时，我们易求出AC及BC的长，然后根据S△ABC=

1

2

AC•BC•sin

π

3

计算出三角形的面积；
（2）我们可以根据S△ABC=

1

2

AC•BC•sin

π

3

，我们可以构造出S关于θ的函数，然后根据三角函数的性质，易得三角形露天活动室的最大面积，及对应θ的值．

解答：解：在△ABC中，

AC

sinθ

=

AB

sin π 3

=

BC

sin(θ+ π 3 )

（2分）
化简得：AC=4

3

•sinθ，BC=4

3

•sin(θ+

π

3

)（3分）
（1）当θ=105°时AC=4

3

•sinθ=4

3

sin105°=4

3

cos15°
BC=4

3

•sin(θ+

π

3

)=4

3

sin165°=4

3

sin15°
所以S△ABC=

1

2

AC•BC•sin

π

3

=3

3

（6分）
（2）S△ABC=

1

2

AC•BC•sin

π

3

=12

3

•sinθ•sin(θ+

π

3

)=12

3

sinθ•(

1

2

sinθ+

3

2

cosθ)
=6

3

(sin2θ+

3

sinθ•cosθ)=6

3

(

1-cos2θ

2

+

3

2

sin2θ)（8分）
=6

3

•[

1

2

+sin(2θ-

π

6

)]
即S△ABC=6

3

•sin(2θ-

π

6

)+3

3

（10分）
所以当2θ-

π

6

=

π

2

，即θ=

π

3

时，（S_△ABC）_max=9

3

（12分）
答：当θ=60^°时，所建造的三角形露天活动室的面积最大．（13分）

点评：本题考查的知识点是在实际问题中建立三角函数模型，及解三角形的应用，其中根据S△ABC=

1

2

AC•BC•sin

π

3

，构造S关于θ的函数解析式，是解答的关键．