题目内容
已知函数![]() 在区间[-1,1),(1,3]内各有一个极值点.
在区间[-1,1),(1,3]内各有一个极值点.
(Ⅰ)求a2-4b的最大值;
(Ⅱ)当a2-4b=8时,设函数y=f(x)在点A(1,f(1))处的切线为l,若在点A处穿过y=f(x)的图象(即动点在点A附近沿曲线y=f(x)运动,经过点A时,从l的一侧进入另一侧),求函数f(x)的表达式.
答案:
解析:
解析:
|
(I)因为函数 设两实根为 (II)解法一:由 因为切线 所以 而 若 所以 解法二:同解法一得 因为切线 当 或当 设 当 或当 由 所以 |

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
 在区间(0,1)内连续,且
在区间(0,1)内连续,且 .
.

 在区间[0,1]上有最小值-2,求
在区间[0,1]上有最小值-2,求 的值.
的值.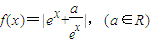 在区间[0,1]上单调递增,则实数a的取值范围是( )
在区间[0,1]上单调递增,则实数a的取值范围是( ) 在区间[0,1]上单调递增,在区间[1,2]上单调递减。
在区间[0,1]上单调递增,在区间[1,2]上单调递减。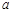 的值;
的值; 的切线,求此直线方程;
的切线,求此直线方程; 的图象与函数
的图象与函数 的图象恰有2个不同交点?若存在,求出实数b的值;若不存在,试说明理由.
的图象恰有2个不同交点?若存在,求出实数b的值;若不存在,试说明理由. 在区间(0,1)内连续,且
在区间(0,1)内连续,且 .
.
