题目内容
已知函数f(x)=|x-a|,g(x)=x2+2ax+1(a为正常数),且函数f(x)与g(x)的图象在y轴上的截距相等.(1)求a的值;
(2)若h(x)=f(x)+b
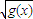 (b为常数),试讨论函数h(x)的奇偶性.
(b为常数),试讨论函数h(x)的奇偶性.
【答案】分析:(1)利用函数f(x)与g(x)的图象在y轴上的截距相等,建立方程,可求a的值;
(2)利用奇偶函数的定义,确定b的值,进而可得函数的奇偶性.
解答:解:(1)由题意,∵函数f(x)与g(x)的图象在y轴上的截距相等,
∴f(0)=g(0),即|a|=1,又a>0,故a=1.(4分)
(2)h(x)=f(x)+b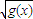 =|x-1|+b|x+1|,其定义域为R,(8分)
=|x-1|+b|x+1|,其定义域为R,(8分)
∴h(-x)=|x+1|+b|x-1|.
若h(x)为偶函数,即h(x)=h(-x),则有b=1,此时h(2)=4,h(-2)=4,
故h(2)≠-h(-2),即h(x)不为奇函数;
若h(x)为奇函数,即h(x)=-h(-x),则b=-1,此时h(2)=2,h(-2)=-2,
故h(2)≠h(-2),即h(x)不为偶函数;
综上,当且仅当b=1时,函数h(x)为偶函数,且不为奇函数,(10分)
当且仅当b=-1时,函数h(x)为奇函数,且不为偶函数,(12分)
当b≠±1时,函数h(x)既非奇函数又非偶函数.(14分)
点评:本题考查函数的性质,考查函数的奇偶性,正确运用函数奇偶性的定义是关键.
(2)利用奇偶函数的定义,确定b的值,进而可得函数的奇偶性.
解答:解:(1)由题意,∵函数f(x)与g(x)的图象在y轴上的截距相等,
∴f(0)=g(0),即|a|=1,又a>0,故a=1.(4分)
(2)h(x)=f(x)+b
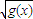 =|x-1|+b|x+1|,其定义域为R,(8分)
=|x-1|+b|x+1|,其定义域为R,(8分)∴h(-x)=|x+1|+b|x-1|.
若h(x)为偶函数,即h(x)=h(-x),则有b=1,此时h(2)=4,h(-2)=4,
故h(2)≠-h(-2),即h(x)不为奇函数;
若h(x)为奇函数,即h(x)=-h(-x),则b=-1,此时h(2)=2,h(-2)=-2,
故h(2)≠h(-2),即h(x)不为偶函数;
综上,当且仅当b=1时,函数h(x)为偶函数,且不为奇函数,(10分)
当且仅当b=-1时,函数h(x)为奇函数,且不为偶函数,(12分)
当b≠±1时,函数h(x)既非奇函数又非偶函数.(14分)
点评:本题考查函数的性质,考查函数的奇偶性,正确运用函数奇偶性的定义是关键.

练习册系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|