题目内容
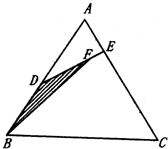 如图所示,已知D是面积为1的△ABC的边AB上的任一点,E是边AC上任一点,连接DE,F是线段DE上一点,连接BF,设
如图所示,已知D是面积为1的△ABC的边AB上的任一点,E是边AC上任一点,连接DE,F是线段DE上一点,连接BF,设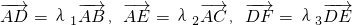 ,且
,且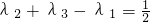 ,则△BDF的面积S的最大值是
,则△BDF的面积S的最大值是
- A.

- B.

- C.

- D.

D
分析:由三角形ABC的面积为1且 可求三角形ADE的面积,再由△DMB∽△DEA可得
可求三角形ADE的面积,再由△DMB∽△DEA可得 从而有
从而有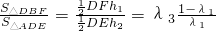 ,求出三角形DEF的面积之后,利用基本不等式可求面积的最大值
,求出三角形DEF的面积之后,利用基本不等式可求面积的最大值
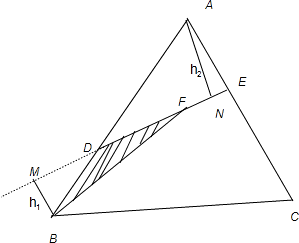
解答:分别过B,A作BM⊥DE,AN⊥DE,垂足分别为M,N,设MB=h1,AN=h2
则
∴S△ADE=λ1λ2S△ABC=λ1λ2
∵△DMB∽△DEA
∴
从而有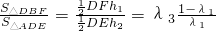
∴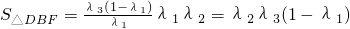 ≤
≤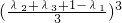 =
=
当且仅当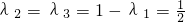 取等号
取等号
故选:D
点评:本题以向量的共线为切入点,利用向量的共线转化为线段的长度关系,解决本题的关键是根据三角形的面积公式先求出三角形ADE的面积;关键二是把所求的三角形的面积与三角形ADE的面积之间通过三角形的像似建立联系.本题是一道构思非常巧妙的试题,要求考试不但要熟练掌握基础知识,更要具备综合解决问题的能力.
分析:由三角形ABC的面积为1且
 可求三角形ADE的面积,再由△DMB∽△DEA可得
可求三角形ADE的面积,再由△DMB∽△DEA可得 从而有
从而有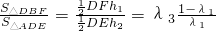 ,求出三角形DEF的面积之后,利用基本不等式可求面积的最大值
,求出三角形DEF的面积之后,利用基本不等式可求面积的最大值解答:分别过B,A作BM⊥DE,AN⊥DE,垂足分别为M,N,设MB=h1,AN=h2
则

∴S△ADE=λ1λ2S△ABC=λ1λ2
∵△DMB∽△DEA
∴

从而有
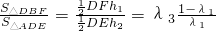
∴
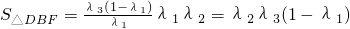 ≤
≤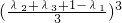 =
=
当且仅当
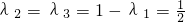 取等号
取等号故选:D

点评:本题以向量的共线为切入点,利用向量的共线转化为线段的长度关系,解决本题的关键是根据三角形的面积公式先求出三角形ADE的面积;关键二是把所求的三角形的面积与三角形ADE的面积之间通过三角形的像似建立联系.本题是一道构思非常巧妙的试题,要求考试不但要熟练掌握基础知识,更要具备综合解决问题的能力.

练习册系列答案
相关题目

 如图所示,已知在直三棱柱ABO-A1B1O1中,∠AOB=
如图所示,已知在直三棱柱ABO-A1B1O1中,∠AOB=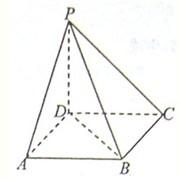 如图所示,已知ABCD是正方形,边长为2,PD⊥平面ABCD.
如图所示,已知ABCD是正方形,边长为2,PD⊥平面ABCD. ,底面边长为
,底面边长为 ,E是SA的中点,则异面直线BE与SC所成角的大小为
( )
,E是SA的中点,则异面直线BE与SC所成角的大小为
( )