题目内容
若0<x<y<1,则
- A.3y<3x
- B.logx3<logy3
- C.log4x<log4y
- D.
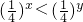
C
分析:根据对数函数的单调性,y=log4x为单调递增函数,可得答案.
解答:∵函数f(x)=log4x为增函数∴log4x<log4y
故选C.
点评:本题主要考查指数函数与对数函数的单调性,即底数大于1时单调递增,底数大于0小于1时单调递减.这也是高考中必考的内容.
分析:根据对数函数的单调性,y=log4x为单调递增函数,可得答案.
解答:∵函数f(x)=log4x为增函数∴log4x<log4y
故选C.
点评:本题主要考查指数函数与对数函数的单调性,即底数大于1时单调递增,底数大于0小于1时单调递减.这也是高考中必考的内容.

练习册系列答案
相关题目
若0<x<y<1,则( )
| A、3y<3x | ||||
| B、logx3<logy3 | ||||
| C、log4x<log4y | ||||
D、(
|
若0<x<y<1,则( )
| A、3y<3x | ||||
B、(
| ||||
| C、logx3<logy3 | ||||
| D、log4x<log4y |