题目内容
全国第十二届全国人民代表大会第二次会议和政协第十二届全国委员会第二次会议,2014年3月在北京开幕.期间为了了解国企员工的工资收入状况,从108名相关人员中用分层抽样方法抽取若干人组成调研小组,有关数据见下表:(单位:人)
| | 相关人数 | 抽取人数 |
| 一般职工 | 63 | 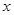 |
| 中层 | 27 | 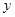 |
| 高管 | 18 | 2 |
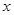 ,
,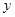 ;
;(2)若从中层、高管抽取的人员中选
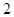 人,求这二人都来自中层的概率.
人,求这二人都来自中层的概率.
(1) 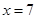 ,
,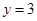 . (2)
. (2)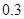 .
.
解析试题分析:(1)由题意可得 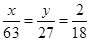 .
.
(2)记从中层抽取的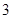 人为
人为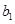 ,
,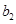 ,
,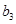 ,从高管抽取的
,从高管抽取的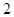 人为
人为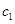 ,
,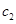 ,
,
用列举法写出抽取的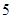 人中选
人中选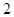 人的基本事件有:
人的基本事件有: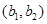 ,
,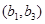 ,
,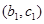 ,
,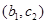 ,
,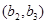 ,
,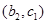 ,
,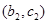 ,
,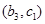 ,
,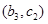 ,
,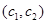 共
共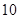 种.
种.
选中的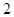 人都来自中层的事件包含的基本事件有:
人都来自中层的事件包含的基本事件有: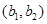 ,
,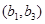 ,
,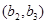 共
共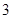 种.
种.
由古典概型概率的计算公式即得.
试题解析:(1)由题意可得 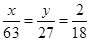 ,所以
,所以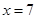 ,
,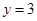 . 3分
. 3分
(2)记从中层抽取的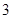 人为
人为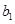 ,
,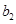 ,
,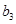 ,从高管抽取的
,从高管抽取的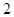 人为
人为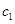 ,
,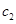 ,
,
则抽取的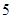 人中选
人中选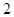 人的基本事件有:
人的基本事件有: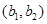 ,
,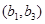 ,
,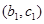 ,
,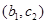 ,
,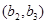 ,
,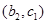 ,
,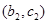 ,
,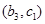 ,
,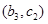 ,
,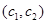 共
共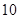 种. 8分
种. 8分
设选中的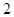 人都来自中层的事件为
人都来自中层的事件为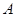 ,
,
则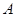 包含的基本事件有:
包含的基本事件有: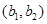 ,
,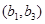 ,
,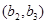 共
共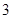 种. 10分
种. 10分
因此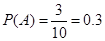 .
.
故选中的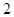 人都来自中层的概率为
人都来自中层的概率为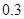 . 12分
. 12分
考点:抽样方法,古典概型.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
为了解甲、乙两个快递公司的工作状况,假设同一个公司快递员的工作状况基本相同,现从甲、乙两公司各随机抽取一名快递员,并从两人某月(30天)的快递件数记录结果中随机抽取10天的数据,制表如下:
| 甲公司某员工A | | 乙公司某员工B | ||||||||||||
| 3 | 9 | 6 | 5 | 8 | 3 | 3 | 2 | 3 | 4 | 6 | 6 | 6 | 7 | 7 |
| | | | | | | 0 | 1 | 4 | 4 | 2 | 2 | 2 | | |
甲公司规定每件4.5元;乙公司规定每天35件以内(含35件)的部分每件4元,超出35件的部分每件7元.
(1)根据表中数据写出甲公司员工A在这10天投递的快递件数的平均数和众数;
(2)为了解乙公司员工B的每天所得劳务费的情况,从这10天中随机抽取1天,他所得的劳务费记为
 (单位:元),求
(单位:元),求 的分布列和数学期望;
的分布列和数学期望;(3)根据表中数据估算两公司的每位员工在该月所得的劳务费.
某医院一天派出医生下乡医疗,派出医生人数及其概率如下:
| 医生人数 | 0 | 1 | 2 | 3 | 4 | 5人及以上 |
| 概率 | 0.1 | 0.16 | x | y | 0.2 | z |
(2)若派出医生最多4人的概率为0.96,最少3人的概率为0.44,求y、z的值.
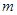 元,正确回答问题B可获奖金
元,正确回答问题B可获奖金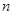 元.活动规定:参与者可任意选择回答问题的顺序,如果第一个问题回答错误,则该参与者猜奖活动中止.假设一个参与者在回答问题前,对这两个问题都很陌生,试确定哪种回答问题的顺序能使该参与者获奖金额的期望值较大.
元.活动规定:参与者可任意选择回答问题的顺序,如果第一个问题回答错误,则该参与者猜奖活动中止.假设一个参与者在回答问题前,对这两个问题都很陌生,试确定哪种回答问题的顺序能使该参与者获奖金额的期望值较大.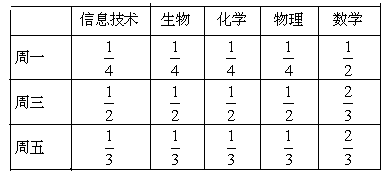
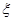 ,求随机变量
,求随机变量