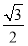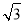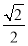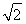题目内容
已知二次函数f(x)=ax2+x,若对任意x1、x2∈R,恒有2f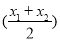 ≤f(x1)+f(x2)成立,不等式f(x)<0的解集为A.
≤f(x1)+f(x2)成立,不等式f(x)<0的解集为A.
(1)求集合A;
(2)设集合B={x||x+4|<a},若集合B是集合A的子集,求a的取值范围.
(1)A= (2)(0,-2+
(2)(0,-2+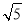 ]
]
【解析】(1)对任意x1、x2∈R,
由f(x1)+f(x2)-2f =
= a(x1-x2)2≥0成立,
a(x1-x2)2≥0成立,
要使上式恒成立,所以a≥0.
由f(x)=ax2+x是二次函数知a≠0,故a>0.
所以f(x)=ax2+x=ax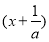 <0.
<0.
解得A= .
.
(2)B={x||x+4|<a}=(-a-4,a-4),
因为集合B是集合A的子集,
所以a-4≤0,且-a-4≥-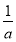 .
.
解得-2- ≤a≤-2+
≤a≤-2+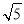 .
.
又a>0,∴a的取值范围为(0,-2+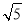 ].
].

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目