题目内容
【题目】如图，设长方体
中，
，
，
是
的中点，点
在线段
上.
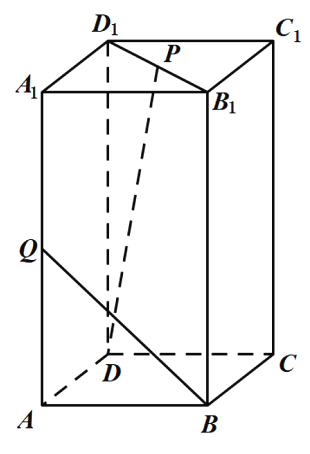
（1）试在线段上确定点的位置，使得异面直线
与
所成角为
，并请说明你的理由；
（2）在满足（1）的条件下，求四棱锥
的体积.
【答案】（1）P是线段
的中点，理由见解析；（2）
.
【解析】
（1）以
为坐标原点，分别以
、
、
所在直线为
、
、
轴建立空间直角坐标系，设
，把
的坐标用
表示，然后分别求出
的坐标，再由
列式求得值得答案；
（2）由图可得四棱锥
的高为
，再求出底面直角梯形的面积，代入棱锥体积公式求得四棱锥的体积．
解：（1）是线段中点．
证明如下：
以为坐标原点，分别以、、所在直线为、、轴建立空间直角坐标系，
则
，0，
，
，0，
，
，1，，
，0，
，
，1，，
设，则
，
，，，
，，，又
，1，
，
．
，解得：
；
（2）连接，则
平面
，
平面，四棱锥的高为
．
．
．
练习册系列答案
相关题目
【题目】某工厂生产一批零件，为了解这批零件的质量状况，检验员从这批产品中随机抽取了100件作为样本进行检测，将它们的重量（单位：g）作为质量指标值．由检测结果得到如下频率分布直方图．
分组 | 频数 | 频率 |
| 8 | |
| ||
| ||
| 16 | 0.16 |
| 4 | 0.04 |
合计 | 100 | 1 |
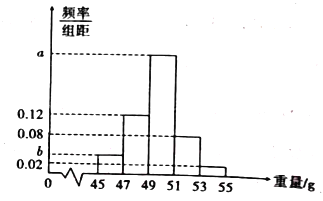
（1）求图中
的值；
（2）根据质量标准规定：零件重量小于47或大于53为不合格品，重量在区间
和
内为合格品，重量在区间
内为优质品．已知每件产品的检测费用为5元，每件不合格品的回收处理费用为20元．以抽检样本重量的频率分布作为该零件重量的概率分布．若这批零件共
件
，现有两种销售方案：方案一：不再检测其他零件，整批零件除对已检测到的不合格品进行回收处理，其余零件均按150元/件售出；方案二：继续对剩余零件的重量进行逐一检测，回收处理所有不合格品，合格品按150元/件售出，优质品按200元/件售出．仅从获得利润大的角度考虑，该生产商应选择哪种方案？请说明理由．
