题目内容
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AB=1,AC=2,BC= ![]() ,D,E分别是AC1和BB1的中点,则直线DE与平面BB1C1C所成的角为( )
,D,E分别是AC1和BB1的中点,则直线DE与平面BB1C1C所成的角为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
【答案】A
【解析】解:取AC的中点为F,连接BF、DF. 因为在直三棱柱ABC﹣A1B1C1中,CC1∥BB1 , 又因为DF是三角形ACC1的中位线,故DF= ![]() CC1=
CC1= ![]() BB1=BE,故四边形BEDF是平行四边形,所以ED∥BF.
BB1=BE,故四边形BEDF是平行四边形,所以ED∥BF.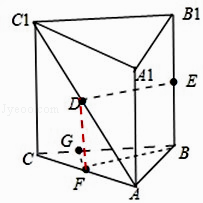
过点F作FG垂直与BC交BC与点G,由题意得∠FBG即为所求的角.
因为AB=1,AC=2,BC= ![]() ,所以∠ABC=
,所以∠ABC= ![]() ,∠BCA=
,∠BCA= ![]() ,直角三角形斜边中线BF是斜边AC的一半,故BF=
,直角三角形斜边中线BF是斜边AC的一半,故BF= ![]() AC=CF,所以
AC=CF,所以
∠FBG=∠BCA= ![]() .
.
故选A.
根据题意得ED∥BF,进而得到直线DE与平面BB1C1C所成的角等于直线BF与平面BB1C1C所成的角.利用几何体的结构特征得到∠FBG= ![]() .即可得到答案.
.即可得到答案.

【题目】某高校在2009年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如图所示. 
(1)请先求出频率分布表中①、②位置相应数据,再在答题纸上完成下列频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官进行面试,求:第4组至少有一名学生被考官A面试的概率?
组号 | 分组 | 频数 | 频率 |
第1组 | [160,165) | 5 | 0.050 |
第2组 | [165,170) | ① | 0.350 |
第3组 | [170,175) | 30 | ② |
第4组 | [175,180) | 20 | 0.200 |
第5组 | [180,185) | 10 | 0.100 |
合计 | 100 | 1.00 | |