题目内容
【题目】已知
为平面内不共线的三点，
表示
的面积
（1）若
求；
（2）若
，
，
，证明:
；
（3）若
，
，
，其中，且坐标原点
恰好为的重心，判断是否为定值，若是，求出该定值；若不是，请说明理由.
【答案】（1）
；（2）详见解析；（3）
是定值，值为
，理由见解析.
【解析】
（1） 已知三点坐标，则可以求出三边长度及对应向量，由向量数量积公式可以求出夹角余弦值，从而算出正弦值，利用面积公式完成作答；
（2） 和（1）的方法一样，唯独不同在于（1）是具体值，而（2）中是参数，我们可以把参数当做整体（视为已知）能处理；
（3） 由
恰好为
的正心可以获取
，而
可以借助（2）的公式直接运用，本题也就完成作答.
（1）因为
，
所以
，
，
所以
因为
，所以
，
所以
（2）因为
，所以
所以
因为
所以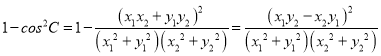
所以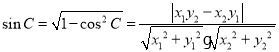
所以
；
（3）因为为的重心，所以
由(1)可知
又因为为的重心，所以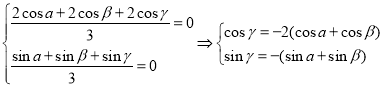
，
平方相加得:
， 即
，
所以
所以
，
所以是定值，值为
练习册系列答案
名校课堂系列答案
相关题目
