题目内容
设函数f(x)=Asin(ωx+φ)A>0,ω>0,|φ|< )的最高点D的坐标为(
)的最高点D的坐标为(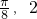 ),由最高点D运动到相邻最低点时,函数图形与x的交点的坐标为(
),由最高点D运动到相邻最低点时,函数图形与x的交点的坐标为(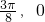 );
);
(1)求函数f(x)的解析式.
(2)当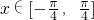 时,求函数f(x)的最大值和最小值以及分别取得最大值和最小值时相应的自变量x的值.
时,求函数f(x)的最大值和最小值以及分别取得最大值和最小值时相应的自变量x的值.
(3)将函数y=f(x)的图象向右平移 个单位,得到函数y=g(x)的图象,求函数y=g(x)的单调减区间.
个单位,得到函数y=g(x)的图象,求函数y=g(x)的单调减区间.
解:(1)∵由最高点D( ,2)运动到相邻最低点时,函数图形与x轴的交点为(
,2)运动到相邻最低点时,函数图形与x轴的交点为( ,0),所以周期的四分之一即
,0),所以周期的四分之一即 =
= -
- =
= ,∴T=π,又T=
,∴T=π,又T= π,∴ω=2,因为函数经过点D的坐标为(
π,∴ω=2,因为函数经过点D的坐标为(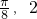 ),代入函数解析式得2sin(2×
),代入函数解析式得2sin(2× +φ)=2,
+φ)=2,
所以2× +φ=
+φ= +2kπ,k∈Z,即φ=zkπ+
+2kπ,k∈Z,即φ=zkπ+ ,k∈Z,又|φ|<
,k∈Z,又|φ|< ,所以φ=
,所以φ= ,
,
∴函数的解析式为f(x)=2sin(2x+ )
)
(2)由(1)知f(x)=2sin(2x+ ),当x∈[-
),当x∈[- ,
, ],2x+
],2x+ ∈[-
∈[- ,
, ]
]
所以2x+ =-
=- ,即x=-
,即x=- 时;函数f(x)有最小值-
时;函数f(x)有最小值-
2x+ =
= ,即x=
,即x= 时;函数f(x)有最大值2
时;函数f(x)有最大值2
(3)由题意g(x)=f(x- )=2sin[2(x-
)=2sin[2(x- )+
)+ ],
],
∴g(x)=2sin(2x- )因为正弦函数y=sinx的减区间是[2kπ+
)因为正弦函数y=sinx的减区间是[2kπ+ ,2kπ+
,2kπ+ ],k∈Z
],k∈Z
所以有2kπ+ ≤2x-
≤2x- ≤2kπ+
≤2kπ+ ,k∈Z,解得kπ+
,k∈Z,解得kπ+ ≤x≤kπ+
≤x≤kπ+ ,k∈Z,
,k∈Z,
故函数g(x)的减区间为[kπ+ ,kπ+
,kπ+ ],k∈Z,
],k∈Z,
分析:(1)由三角函数解析式可知函数的平衡位置在x轴,所以最高点的纵坐标为A=2,又由于三角函数最高点与相邻的和x轴的交点为周期的四分之一,即 =
=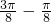 ,借此求出周期后可求出ω的值,然后将点(
,借此求出周期后可求出ω的值,然后将点( ,2)代入函数解析式并结合|φ|<
,2)代入函数解析式并结合|φ|< 可求出φ的值.
可求出φ的值.
(2)由题中x的范围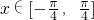 可求出(1)中解析式里2x+
可求出(1)中解析式里2x+ 的范围,然后结合正弦函数y=sinx相应区间上的图象可以确定当2x+
的范围,然后结合正弦函数y=sinx相应区间上的图象可以确定当2x+ =-
=- 和2x+
和2x+ =
= 时函数分别有最小值与最大值,并同时解出相应x的取值即可.
时函数分别有最小值与最大值,并同时解出相应x的取值即可.
(3)由于函数图象左右平移改变的是横坐标,为此将函数y=f(x)的图象向右平移 个单位后应用函数解析式中的自变量x
个单位后应用函数解析式中的自变量x ,即y=g(x)=2sin[2(x
,即y=g(x)=2sin[2(x )+
)+ ]=2sin(2x-
]=2sin(2x- ),由于求的是函数g(x)的减区间,故用2x-
),由于求的是函数g(x)的减区间,故用2x- 替换正弦函数的减区间即由2kπ
替换正弦函数的减区间即由2kπ ≤2x-
≤2x- ≤2kπ+
≤2kπ+ ,k∈Z解出x后就是所求的减区间.
,k∈Z解出x后就是所求的减区间.
点评:本题主要考查了复合角三角函数的解析式,最值以及图象变换和单调区间的求法等问题,属于复合角三角函数的性质的综合性命题.
 ,2)运动到相邻最低点时,函数图形与x轴的交点为(
,2)运动到相邻最低点时,函数图形与x轴的交点为( ,0),所以周期的四分之一即
,0),所以周期的四分之一即 =
= -
- =
= ,∴T=π,又T=
,∴T=π,又T= π,∴ω=2,因为函数经过点D的坐标为(
π,∴ω=2,因为函数经过点D的坐标为(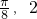 ),代入函数解析式得2sin(2×
),代入函数解析式得2sin(2× +φ)=2,
+φ)=2,所以2×
 +φ=
+φ= +2kπ,k∈Z,即φ=zkπ+
+2kπ,k∈Z,即φ=zkπ+ ,k∈Z,又|φ|<
,k∈Z,又|φ|< ,所以φ=
,所以φ= ,
,∴函数的解析式为f(x)=2sin(2x+
 )
)(2)由(1)知f(x)=2sin(2x+
 ),当x∈[-
),当x∈[- ,
, ],2x+
],2x+ ∈[-
∈[- ,
, ]
]所以2x+
 =-
=- ,即x=-
,即x=- 时;函数f(x)有最小值-
时;函数f(x)有最小值-
2x+
 =
= ,即x=
,即x= 时;函数f(x)有最大值2
时;函数f(x)有最大值2(3)由题意g(x)=f(x-
 )=2sin[2(x-
)=2sin[2(x- )+
)+ ],
],∴g(x)=2sin(2x-
 )因为正弦函数y=sinx的减区间是[2kπ+
)因为正弦函数y=sinx的减区间是[2kπ+ ,2kπ+
,2kπ+ ],k∈Z
],k∈Z所以有2kπ+
 ≤2x-
≤2x- ≤2kπ+
≤2kπ+ ,k∈Z,解得kπ+
,k∈Z,解得kπ+ ≤x≤kπ+
≤x≤kπ+ ,k∈Z,
,k∈Z,故函数g(x)的减区间为[kπ+
 ,kπ+
,kπ+ ],k∈Z,
],k∈Z,分析:(1)由三角函数解析式可知函数的平衡位置在x轴,所以最高点的纵坐标为A=2,又由于三角函数最高点与相邻的和x轴的交点为周期的四分之一,即
 =
=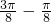 ,借此求出周期后可求出ω的值,然后将点(
,借此求出周期后可求出ω的值,然后将点( ,2)代入函数解析式并结合|φ|<
,2)代入函数解析式并结合|φ|< 可求出φ的值.
可求出φ的值.(2)由题中x的范围
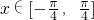 可求出(1)中解析式里2x+
可求出(1)中解析式里2x+ 的范围,然后结合正弦函数y=sinx相应区间上的图象可以确定当2x+
的范围,然后结合正弦函数y=sinx相应区间上的图象可以确定当2x+ =-
=- 和2x+
和2x+ =
= 时函数分别有最小值与最大值,并同时解出相应x的取值即可.
时函数分别有最小值与最大值,并同时解出相应x的取值即可.(3)由于函数图象左右平移改变的是横坐标,为此将函数y=f(x)的图象向右平移
 个单位后应用函数解析式中的自变量x
个单位后应用函数解析式中的自变量x ,即y=g(x)=2sin[2(x
,即y=g(x)=2sin[2(x )+
)+ ]=2sin(2x-
]=2sin(2x- ),由于求的是函数g(x)的减区间,故用2x-
),由于求的是函数g(x)的减区间,故用2x- 替换正弦函数的减区间即由2kπ
替换正弦函数的减区间即由2kπ ≤2x-
≤2x- ≤2kπ+
≤2kπ+ ,k∈Z解出x后就是所求的减区间.
,k∈Z解出x后就是所求的减区间.点评:本题主要考查了复合角三角函数的解析式,最值以及图象变换和单调区间的求法等问题,属于复合角三角函数的性质的综合性命题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (n∈N*)
(n∈N*) .
. 对不小于2的正整数恒成立,求x的取值范围.
对不小于2的正整数恒成立,求x的取值范围.