题目内容
设a∈(0,1),则关于x的不等式|x-logax|<|x|+|logax|的解集是( )
分析:由绝对值不等式的性质,结合题意可得x与logax符号相同,从而得到logax>0,根据a∈(0,1)可得原不等式的解集.
解答:解:由绝对值不等式的性质,可得|x-logax|≤|x|+|logax|,
当且仅当x与logax符号相异,即一正一负时,等号成立.
∵由题意知|x-logax|<|x|+|logax|,∴等号不成立,可知x与logax符号相同,
∵在logax中,x为正数,∴logax>0
结合a∈(0,1),可得0<x<1,原不等式的解集为(0,1).
故选:B
当且仅当x与logax符号相异,即一正一负时,等号成立.
∵由题意知|x-logax|<|x|+|logax|,∴等号不成立,可知x与logax符号相同,
∵在logax中,x为正数,∴logax>0
结合a∈(0,1),可得0<x<1,原不等式的解集为(0,1).
故选:B
点评:本题给出含有对数式的绝对值不等式,求不等式的解集.着重考查了对数函数的性质、绝对值不等式的性质和不等式的解法等知识,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设a∈(0,1),则函数y=
的定义域是( )
| loga(x-1) |
| A、(1,2] |
| B、(1,+∞) |
| C、[2,+∞) |
| D、(-∞,2] |
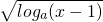 的定义域是
的定义域是 的定义域是( )
的定义域是( )