题目内容
用数学归纳法证“1-
+
-
+…+
-
=
+
+…+
(n∈N*)”的过程中,当n=k到n=k+1时,左边所增加的项为( )
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2n-1 |
| 1 |
| 2n |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2n |
A、-
| ||||
B、
| ||||
C、
| ||||
D、-
|
分析:本题考查的知识点是数学归纳法的过程及步骤,观察到“1-
+
-
+…+
-
=
+
+…+
(n∈N*)”左边是从1开始到n结束,但每个n值对应
-
两项,则当n=k到n=k+1时,左边应增加两项,分别是n=k+1时对应
-
即
-
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2n-1 |
| 1 |
| 2n |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2n |
| 1 |
| 2n-1 |
| 1 |
| 2n |
| 1 |
| 2n-1 |
| 1 |
| 2n |
| 1 |
| 2k+1 |
| 1 |
| 2k+2 |
解答:解:当n=k到n=k+1时,
左边增加了两项
,
,
减少了一项
,
左边所增加的项为
+
-
=
-
.
故选C
左边增加了两项
| 1 |
| 2k+1 |
| 1 |
| 2k+2 |
减少了一项
| 1 |
| k+1 |
左边所增加的项为
| 1 |
| 2k+1 |
| 1 |
| 2k+2 |
| 1 |
| k+1 |
| 1 |
| 2k+1 |
| 1 |
| 2k+2 |
故选C
点评:数学归纳法常常用来证明一个与自然数集N相关的性质,其步骤为:设P(n)是关于自然数n的命题,若1)(奠基) P(n)在n=1时成立;2)(归纳) 在P(k)(k为任意自然数)成立的假设下可以推出P(k+1)成立,则P(n)对一切自然数n都成立.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 +
+ -
- +…+
+…+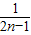 -
- =
=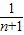 +
+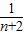 +…+
+…+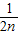 (n∈N*)”的过程中,当n=k到n=k+1时,左边所增加的项为( )
(n∈N*)”的过程中,当n=k到n=k+1时,左边所增加的项为( )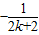
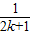
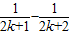

 +
+ -
- +L+
+L+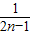 -
-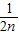 =
=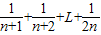 的过程中,当n=k到n=k+1时,左边所增加的项为 .
的过程中,当n=k到n=k+1时,左边所增加的项为 .