题目内容
函数f(x)=lnx- 的零点一定位于区间( )
的零点一定位于区间( )
A.( ,1) ,1) | B.(1,2) | C.(2,e) | D.(e,3) |
C
解析试题分析:因为f(2)=ln2-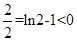 ,f(e)=lne-
,f(e)=lne- , f(2) f(e)<0,所以函数f(x)=lnx-
, f(2) f(e)<0,所以函数f(x)=lnx- 的零点一定位于区间(2,e)。
的零点一定位于区间(2,e)。
考点:函数的零点;零点存在性定理。
点评:零点存在性定理只能判断是否存在零点,而不能判断零点的个数。

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
已知幂函数 的图像经过点
的图像经过点 ,则
,则 的值等于
的值等于
| A.16 | B. | C.2 | D. |
对于使 成立的所有常数
成立的所有常数 中,我们把
中,我们把 的最小值1叫做
的最小值1叫做 的上确界,若
的上确界,若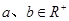 ,且
,且 ,则
,则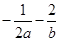 的上确界为( )
的上确界为( )
A. | B. | C. | D.-4 |
函数f(x)= 若方程f(x)=x+a有且只有两个不等的实数根,则实数a的取值范围为
若方程f(x)=x+a有且只有两个不等的实数根,则实数a的取值范围为
| A.(-∞,0) | B.[0,1) | C.(-∞,1) | D.[0,+∞) |
若 是偶函数,其定义域为
是偶函数,其定义域为 ,且在
,且在 上是减函数,则
上是减函数,则 的大小关系是( )
的大小关系是( )
A. > >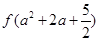 | B. < <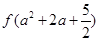 |
C.  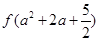 | D.  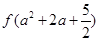 |
函数y=lgx- 的零点所在的大致区间是
的零点所在的大致区间是
| A.(6,7) | B.(7,8) | C.(8,9) | D.(9,10) |
已知三个数 ,则三个数的大小关系是( )
,则三个数的大小关系是( )
A. | B. |
C. | D. |

 的零点个数为
的零点个数为
| A.3 | B.2 | C.1 | D.0 |
设函数 ,若
,若 ,则实数
,则实数 的取值范围是
的取值范围是
A. | B. | C. | D. |