题目内容
本题满分14分)已知函数![]() ,
,![]() ,其中
,其中![]() .w.w.w.k.s.5.u.c.o.m
.w.w.w.k.s.5.u.c.o.m ![]()
![]()
(I)设函数![]() .若
.若![]() 在区间
在区间![]() 上不单调,求
上不单调,求![]() 的取值范围;
的取值范围;
(II)设函数![]() 是否存在
是否存在![]() ,对任意给定的非零实数
,对任意给定的非零实数![]() ,存在惟一的非零实数
,存在惟一的非零实数![]() (
(![]() ),使得
),使得![]() 成立?若存在,求
成立?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
解析:(I)因![]() ,
,![]() ,因
,因![]() 在区间
在区间![]() 上不单调,所以
上不单调,所以![]() 在
在![]() 上有实数解,且无重根,由
上有实数解,且无重根,由![]() 得
得![]() w.w.w.k.s.5.u.c.o.m
w.w.w.k.s.5.u.c.o.m ![]()
![]()
![]() ,令
,令![]() 有
有![]() ,记
,记![]() 则
则![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,所以有
上单调递增,所以有![]() ,于是
,于是![]() ,得
,得![]() ,而当
,而当![]() 时有
时有![]() 在
在![]() 上有两个相等的实根
上有两个相等的实根![]() ,故舍去,所以
,故舍去,所以![]() ;w.w.w.k.s.5.u.c.o.m
;w.w.w.k.s.5.u.c.o.m ![]()
![]()
(II)当![]() 时有
时有![]() ;
;
当![]() 时有
时有![]() ,因为当
,因为当![]() 时不合题意,因此
时不合题意,因此![]() ,
,
下面讨论![]() 的情形,记A
的情形,记A![]() ,B=
,B=![]() ()当
()当![]() 时,
时,![]() 在
在![]() 上单调递增,所以要使
上单调递增,所以要使![]() 成立,只能
成立,只能![]() 且
且![]() ,因此有
,因此有![]() ,()当
,()当![]() 时,
时,![]() 在
在![]() 上单调递减,所以要使
上单调递减,所以要使![]() 成立,只能
成立,只能![]() 且
且![]() ,因此
,因此![]() ,综合()()
,综合()()![]() ;
;
当![]() 时A=B,则
时A=B,则![]() ,即
,即![]() 使得
使得![]() 成立,因为
成立,因为![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() 的值是唯一的;
的值是唯一的;
同理,![]() ,即存在唯一的非零实数
,即存在唯一的非零实数![]() ,要使
,要使![]() 成立,所以
成立,所以![]() 满足题意.w.w.w.k.s.5.u.c.o.m
满足题意.w.w.w.k.s.5.u.c.o.m ![]()
![]()

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
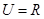 ,集合
,集合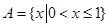 ,
,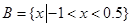 ,求:
,求: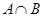 及
及 ;
;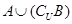 .
.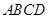 满足
满足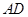 ∥
∥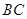 ,
,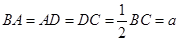 ,
,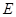 是
是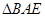 沿着
沿着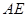 翻折成
翻折成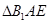 ,使面
,使面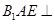 面
面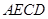 ,
,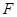 为
为 的中点.
的中点. 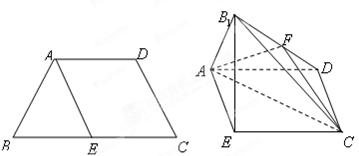
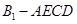 的体积;(Ⅱ)证明:
的体积;(Ⅱ)证明: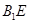 ∥面
∥面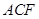 ;
;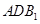 与面
与面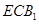 所成二面角的余弦值.
所成二面角的余弦值.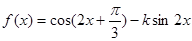 ,且
,且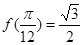 .
.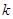 的值;
的值;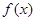 的单调递增区间及最大值,并指出取得最大值时的
的单调递增区间及最大值,并指出取得最大值时的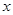 值.
值. 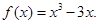
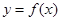 在点
在点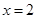 处的切线方程;
处的切线方程;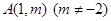 可作曲线
可作曲线 的取值范围.
的取值范围.